Data assimilation in Agent-based models using creation and annihilation operators
Paper and Code
Oct 08, 2019
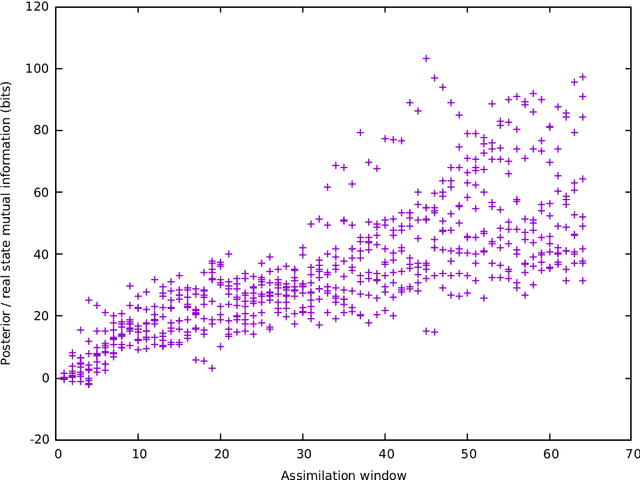
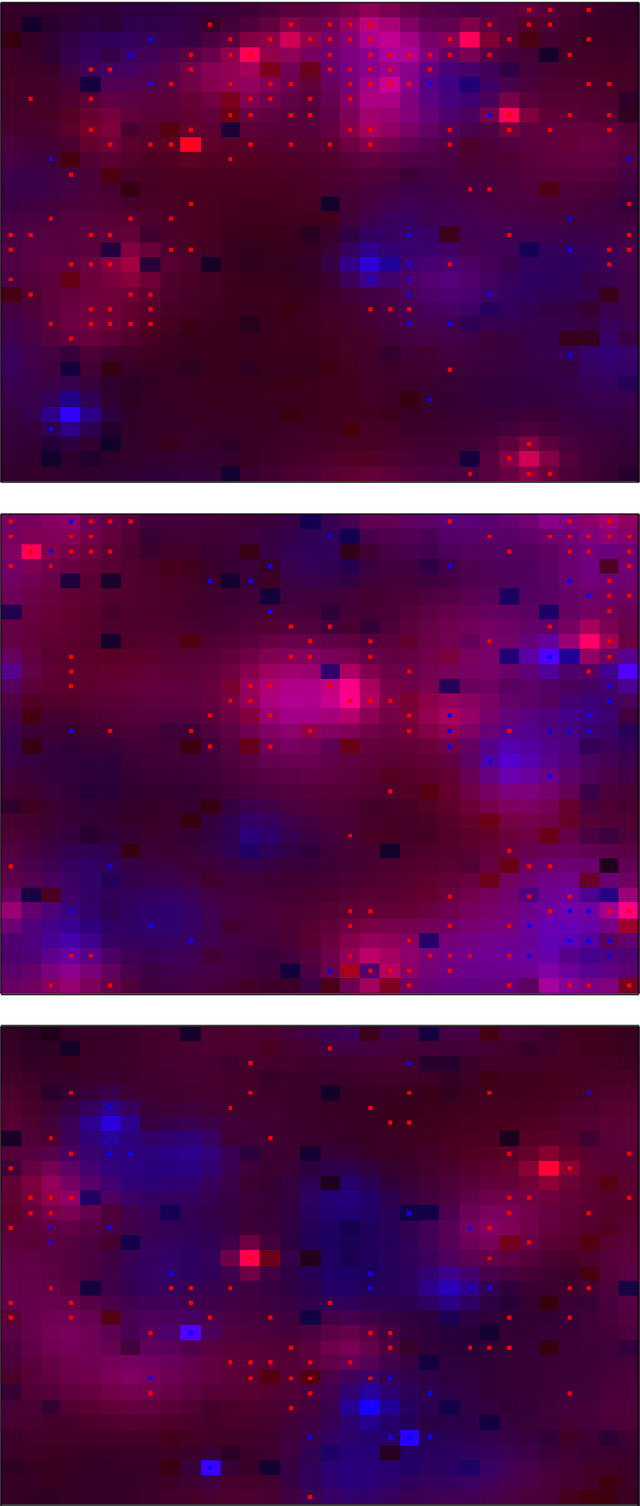
Agent-based models are a powerful tool for studying the behaviour of complex systems that can be described in terms of multiple, interacting ``agents''. However, because of their inherently discrete and often highly non-linear nature, it is very difficult to reason about the relationship between the state of the model, on the one hand, and our observations of the real world on the other. In this paper we consider agents that have a discrete set of states that, at any instant, act with a probability that may depend on the environment or the state of other agents. Given this, we show how the mathematical apparatus of quantum field theory can be used to reason probabilistically about the state and dynamics the model, and describe an algorithm to update our belief in the state of the model in the light of new, real-world observations. Using a simple predator-prey model on a 2-dimensional spatial grid as an example, we demonstrate the assimilation of incomplete, noisy observations and show that this leads to an increase in the mutual information between the actual state of the observed system and the posterior distribution given the observations, when compared to a null model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge