Cutset Sampling with Likelihood Weighting
Paper and Code
Jun 27, 2012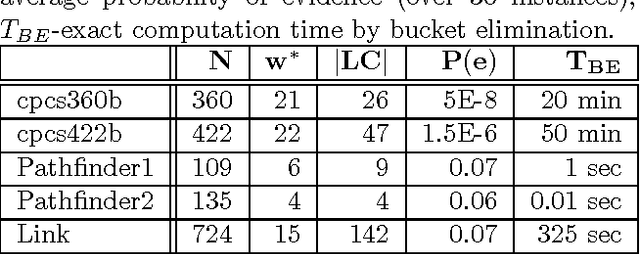
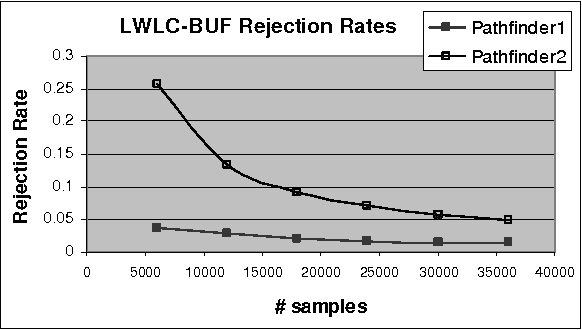
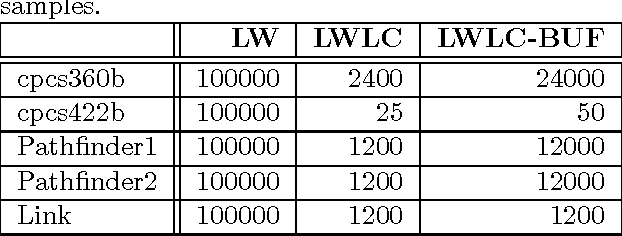
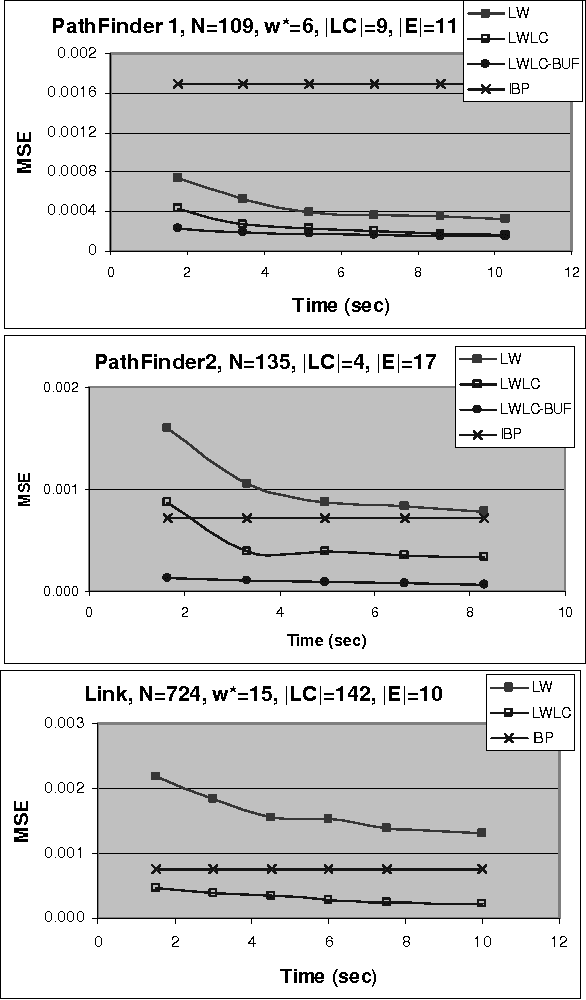
The paper analyzes theoretically and empirically the performance of likelihood weighting (LW) on a subset of nodes in Bayesian networks. The proposed scheme requires fewer samples to converge due to reduction in sampling variance. The method exploits the structure of the network to bound the complexity of exact inference used to compute sampling distributions, similar to Gibbs cutset sampling. Yet, the extension of the previosly proposed cutset sampling principles to likelihood weighting is non-trivial due to differences in the sampling processes of Gibbs sampler and LW. We demonstrate empirically that likelihood weighting on a cutset (LWLC) is effective time-wise and has a lower rejection rate than LW when applied to networks with many deterministic probabilities. Finally, we show that the performance of likelihood weighting on a cutset can be improved further by caching computed sampling distributions and, consequently, learning 'zeros' of the target distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge