Critically Damped Third-Order Langevin Dynamics
Paper and Code
Sep 12, 2024

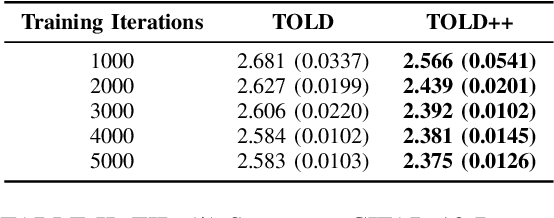

While systems analysis has been studied for decades in the context of control theory, it has only been recently used to improve the convergence of Denoising Diffusion Probabilistic Models. This work describes a novel improvement to Third- Order Langevin Dynamics (TOLD), a recent diffusion method that performs better than its predecessors. This improvement, abbreviated TOLD++, is carried out by critically damping the TOLD forward transition matrix similarly to Dockhorn's Critically-Damped Langevin Dynamics (CLD). Specifically, it exploits eigen-analysis of the forward transition matrix to derive the optimal set of dynamics under the original TOLD scheme. TOLD++ is theoretically guaranteed to converge faster than TOLD, and its faster convergence is verified on the Swiss Roll toy dataset and CIFAR-10 dataset according to the FID metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge