Correlated signal inference by free energy exploration
Paper and Code
Feb 13, 2017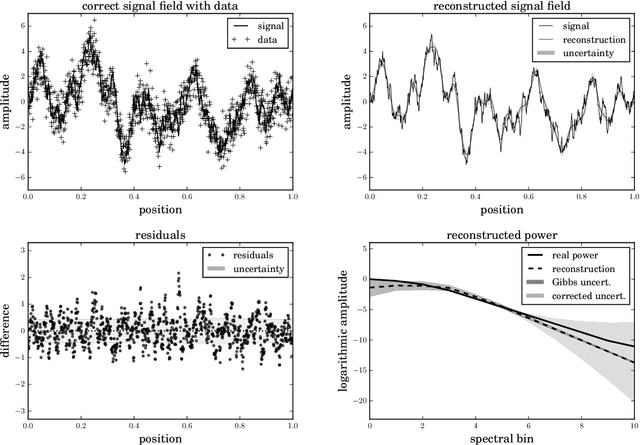
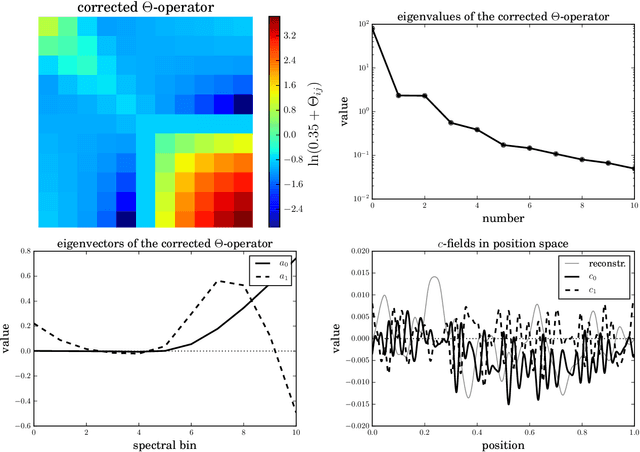
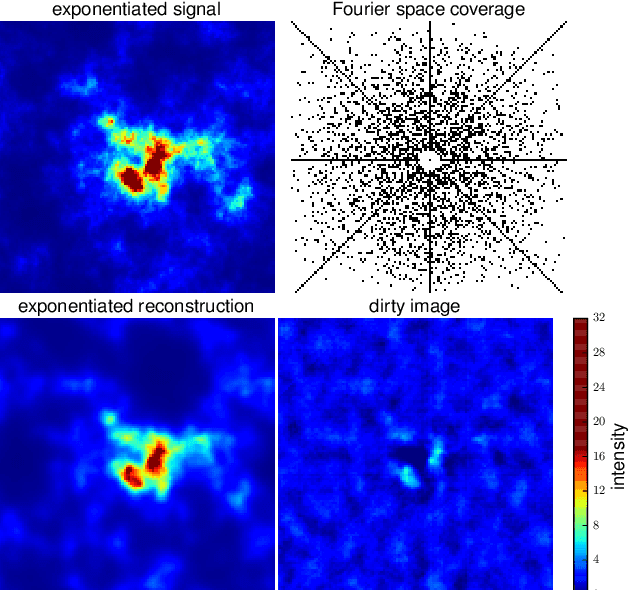
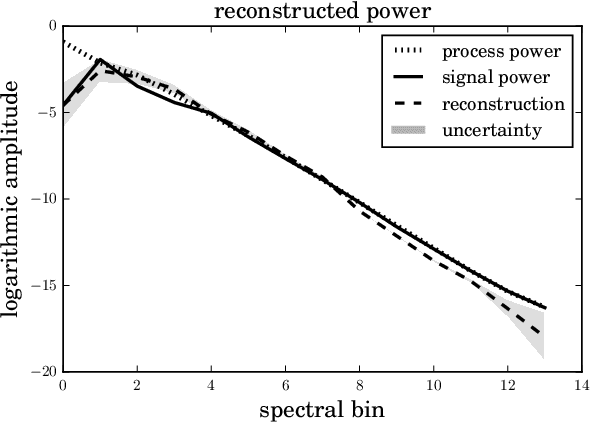
The inference of correlated signal fields with unknown correlation structures is of high scientific and technological relevance, but poses significant conceptual and numerical challenges. To address these, we develop the correlated signal inference (CSI) algorithm within information field theory (IFT) and discuss its numerical implementation. To this end, we introduce the free energy exploration (FrEE) strategy for numerical information field theory (NIFTy) applications. The FrEE strategy is to let the mathematical structure of the inference problem determine the dynamics of the numerical solver. FrEE uses the Gibbs free energy formalism for all involved unknown fields and correlation structures without marginalization of nuisance quantities. It thereby avoids the complexity marginalization often impose to IFT equations. FrEE simultaneously solves for the mean and the uncertainties of signal, nuisance, and auxiliary fields, while exploiting any analytically calculable quantity. Finally, FrEE uses a problem specific and self-tuning exploration strategy to swiftly identify the optimal field estimates as well as their uncertainty maps. For all estimated fields, properly weighted posterior samples drawn from their exact, fully non-Gaussian distributions can be generated. Here, we develop the FrEE strategies for the CSI of a normal, a log-normal, and a Poisson log-normal IFT signal inference problem and demonstrate their performances via their NIFTy implementations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge