Convergence Problems with Generative Adversarial Networks (GANs)
Paper and Code
Jun 29, 2018

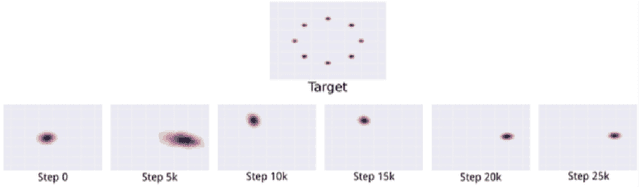

Generative adversarial networks (GANs) are a novel approach to generative modelling, a task whose goal it is to learn a distribution of real data points. They have often proved difficult to train: GANs are unlike many techniques in machine learning, in that they are best described as a two-player game between a discriminator and generator. This has yielded both unreliability in the training process, and a general lack of understanding as to how GANs converge, and if so, to what. The purpose of this dissertation is to provide an account of the theory of GANs suitable for the mathematician, highlighting both positive and negative results. This involves identifying the problems when training GANs, and how topological and game-theoretic perspectives of GANs have contributed to our understanding and improved our techniques in recent years.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge