Continuous-time Infinite Dynamic Topic Models

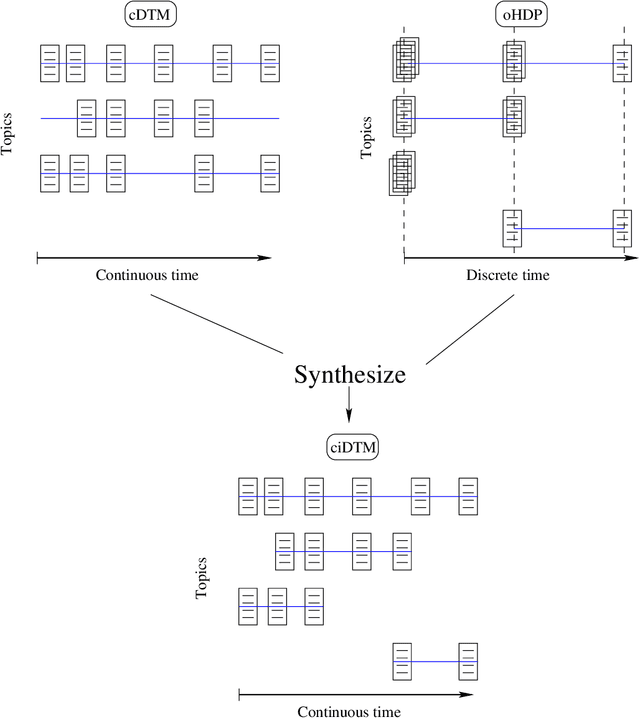
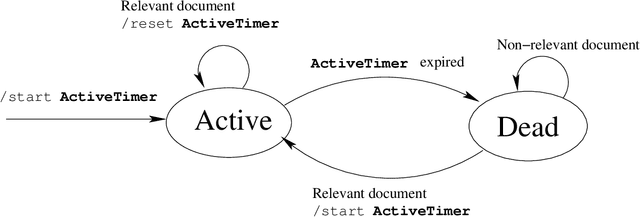
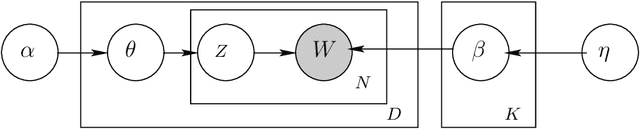
Topic models are probabilistic models for discovering topical themes in collections of documents. In real world applications, these models provide us with the means of organizing what would otherwise be unstructured collections. They can help us cluster a huge collection into different topics or find a subset of the collection that resembles the topical theme found in an article at hand. The first wave of topic models developed were able to discover the prevailing topics in a big collection of documents spanning a period of time. It was later realized that these time-invariant models were not capable of modeling 1) the time varying number of topics they discover and 2) the time changing structure of these topics. Few models were developed to address this two deficiencies. The online-hierarchical Dirichlet process models the documents with a time varying number of topics. It varies the structure of the topics over time as well. However, it relies on document order, not timestamps to evolve the model over time. The continuous-time dynamic topic model evolves topic structure in continuous-time. However, it uses a fixed number of topics over time. In this dissertation, I present a model, the continuous-time infinite dynamic topic model, that combines the advantages of these two models 1) the online-hierarchical Dirichlet process, and 2) the continuous-time dynamic topic model. More specifically, the model I present is a probabilistic topic model that does the following: 1) it changes the number of topics over continuous time, and 2) it changes the topic structure over continuous-time. I compared the model I developed with the two other models with different setting values. The results obtained were favorable to my model and showed the need for having a model that has a continuous-time varying number of topics and topic structure.