Constrained Nonnegative Matrix Factorization for Blind Hyperspectral Unmixing incorporating Endmember Independence
Paper and Code
Apr 03, 2020
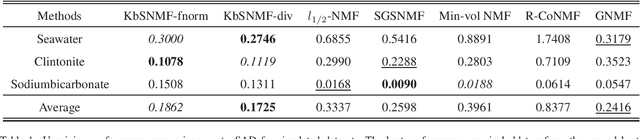
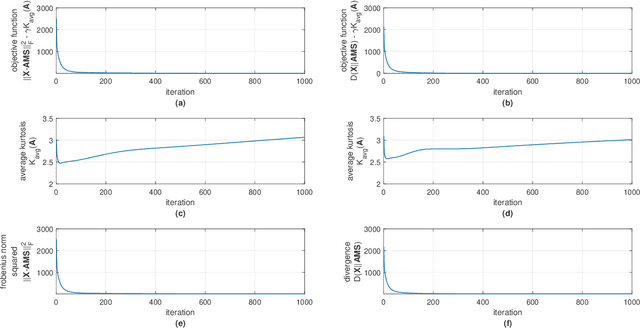
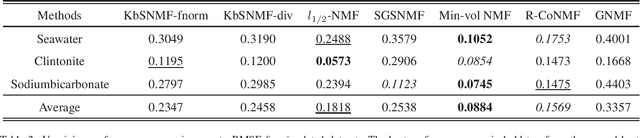
Hyperspectral unmixing (HU) has become an important technique in exploiting hyperspectral data since it decomposes a mixed pixel into a collection of endmember spectra weighted by fractional abundances. The endmembers of a hyperspectral image (HSI) are more likely to be generated by independent sources and be mixed in a macroscopic degree before arriving at the sensor element of the imaging spectrometer as mixed spectra. Over the past few decades, many attempts have focused on imposing auxiliary constraints on the conventional nonnegative matrix factorization (NMF) framework in order to effectively unmix these mixed spectra. As a promising step toward finding an optimum constraint to extract endmembers, this paper presents a novel blind HU algorithm, referred to as Kurtosis-based Smooth Nonnegative Matrix Factorization (KbSNMF) which incorporates a novel constraint based on the statistical independence of the probability density functions of endmember spectra. Imposing this constraint on the conventional NMF framework promotes the extraction of independent endmembers while further enhancing the parts-based representation of data. The proposed algorithm manages to outperform state of the art NMF-based algorithms in terms of extracting endmember spectra from hyperspectral data; therefore, it could uplift the performance of recent deep learning HU methods which utilizes the endmember spectra as supervisory input data for abundance extraction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge