Confidence Sets for the Source of a Diffusion in Regular Trees
Paper and Code
Oct 19, 2015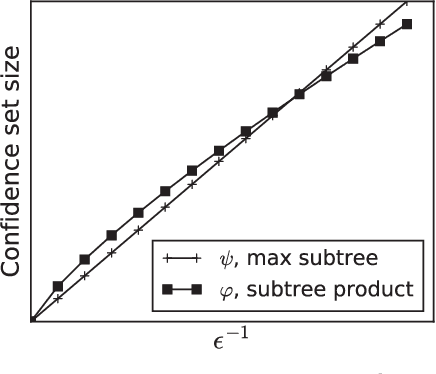

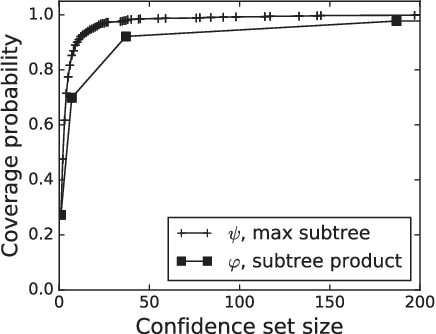
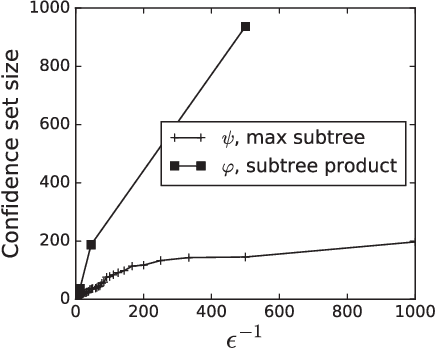
We study the problem of identifying the source of a diffusion spreading over a regular tree. When the degree of each node is at least three, we show that it is possible to construct confidence sets for the diffusion source with size independent of the number of infected nodes. Our estimators are motivated by analogous results in the literature concerning identification of the root node in preferential attachment and uniform attachment trees. At the core of our proofs is a probabilistic analysis of P\'{o}lya urns corresponding to the number of uninfected neighbors in specific subtrees of the infection tree. We also provide an example illustrating the shortcomings of source estimation techniques in settings where the underlying graph is asymmetric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge