Conditional information and definition of neighbor in categorical random fields
Paper and Code
Dec 31, 2010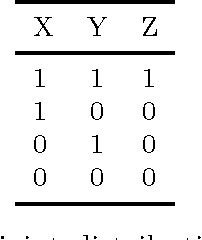
We show that the definition of neighbor in Markov random fields as defined by Besag (1974) when the joint distribution of the sites is not positive is not well-defined. In a random field with finite number of sites we study the conditions under which giving the value at extra sites will change the belief of an agent about one site. Also the conditions under which the information from some sites is equivalent to giving the value at all other sites is studied. These concepts provide an alternative to the concept of neighbor for general case where the positivity condition of the joint does not hold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge