Concept and Attribute Reduction Based on Rectangle Theory of Formal Concept
Paper and Code
Oct 29, 2021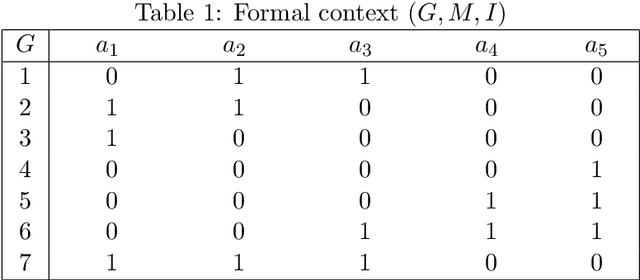


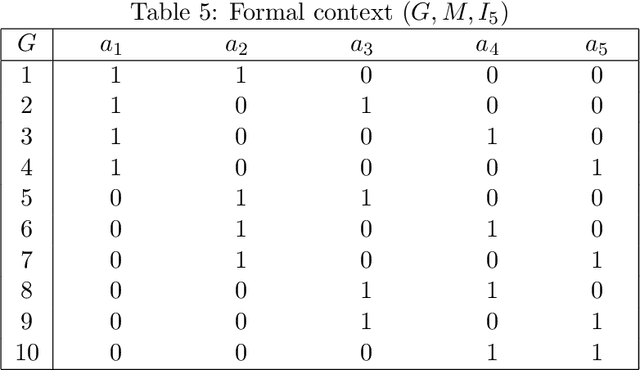
Based on rectangle theory of formal concept and set covering theory, the concept reduction preserving binary relations is investigated in this paper. It is known that there are three types of formal concepts: core concepts, relative necessary concepts and unnecessary concepts. First, we present the new judgment results for relative necessary concepts and unnecessary concepts. Second, we derive the bounds for both the maximum number of relative necessary concepts and the maximum number of unnecessary concepts and it is a difficult problem as either in concept reduction preserving binary relations or attribute reduction of decision formal contexts, the computation of formal contexts from formal concepts is a challenging problem. Third, based on rectangle theory of formal concept, a fast algorithm for reducing attributes while preserving the extensions for a set of formal concepts is proposed using the extension bit-array technique, which allows multiple context cells to be processed by a single 32-bit or 64-bit operator. Technically, the new algorithm could store both formal context and extent of a concept as bit-arrays, and we can use bit-operations to process set operations "or" as well as "and". One more merit is that the new algorithm does not need to consider other concepts in the concept lattice, thus the algorithm is explicit to understand and fast. Experiments demonstrate that the new algorithm is effective in the computation of attribute reductions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge