Complexity of Non-Monotonic Logics
Paper and Code
Sep 10, 2010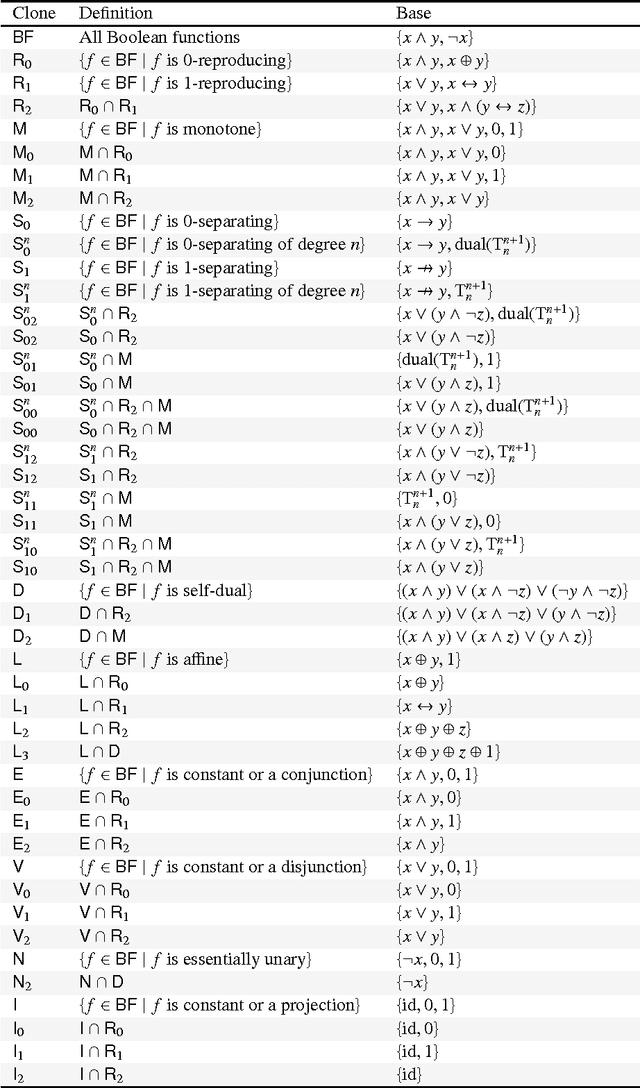
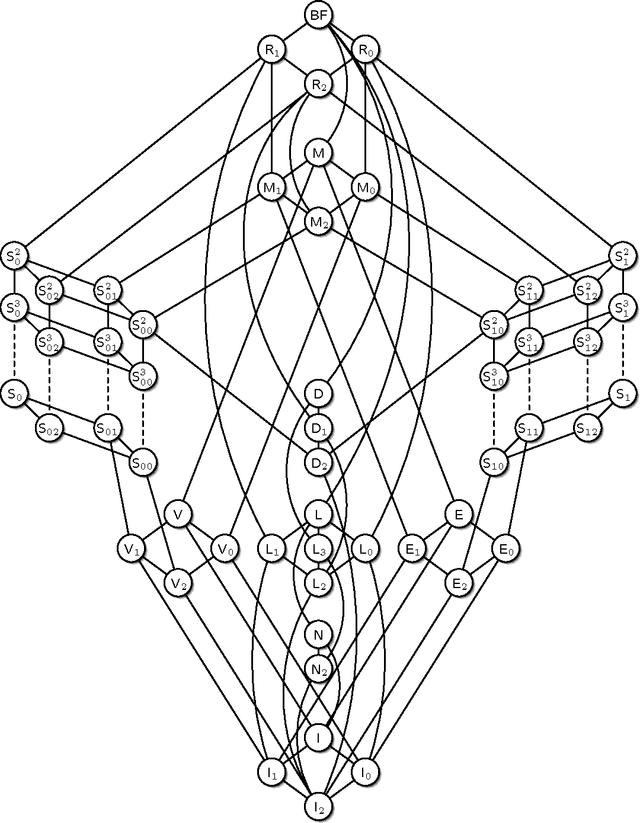
Over the past few decades, non-monotonic reasoning has developed to be one of the most important topics in computational logic and artificial intelligence. Different ways to introduce non-monotonic aspects to classical logic have been considered, e.g., extension with default rules, extension with modal belief operators, or modification of the semantics. In this survey we consider a logical formalism from each of the above possibilities, namely Reiter's default logic, Moore's autoepistemic logic and McCarthy's circumscription. Additionally, we consider abduction, where one is not interested in inferences from a given knowledge base but in computing possible explanations for an observation with respect to a given knowledge base. Complexity results for different reasoning tasks for propositional variants of these logics have been studied already in the nineties. In recent years, however, a renewed interest in complexity issues can be observed. One current focal approach is to consider parameterized problems and identify reasonable parameters that allow for FPT algorithms. In another approach, the emphasis lies on identifying fragments, i.e., restriction of the logical language, that allow more efficient algorithms for the most important reasoning tasks. In this survey we focus on this second aspect. We describe complexity results for fragments of logical languages obtained by either restricting the allowed set of operators (e.g., forbidding negations one might consider only monotone formulae) or by considering only formulae in conjunctive normal form but with generalized clause types. The algorithmic problems we consider are suitable variants of satisfiability and implication in each of the logics, but also counting problems, where one is not only interested in the existence of certain objects (e.g., models of a formula) but asks for their number.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge