Competition analysis on the over-the-counter credit default swap market

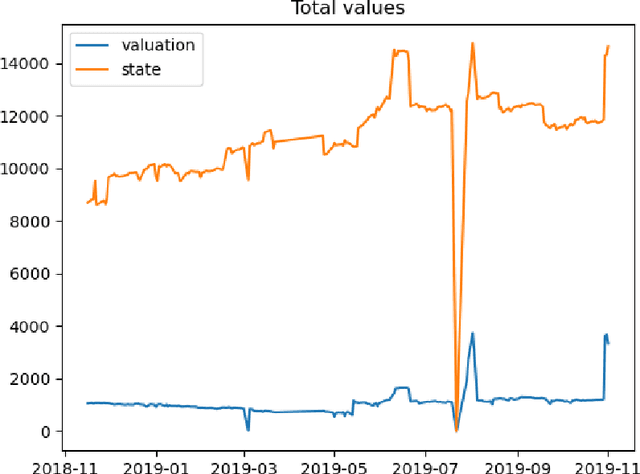
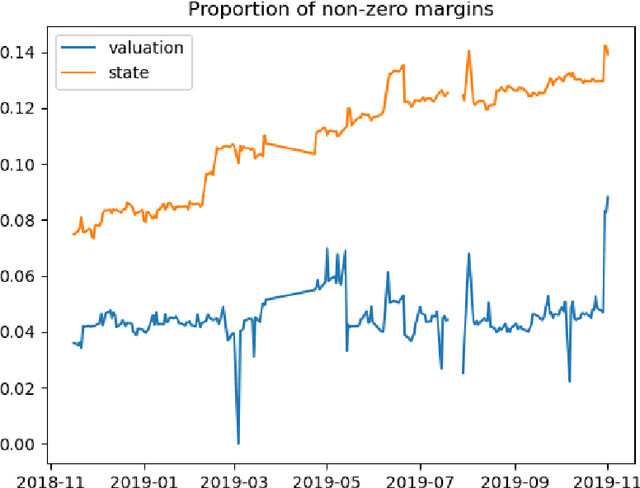
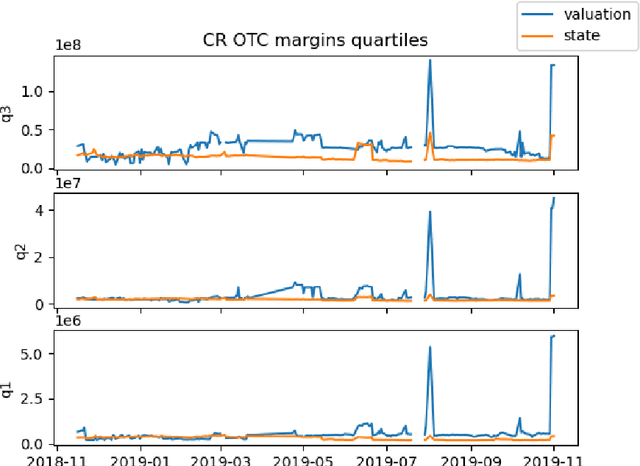
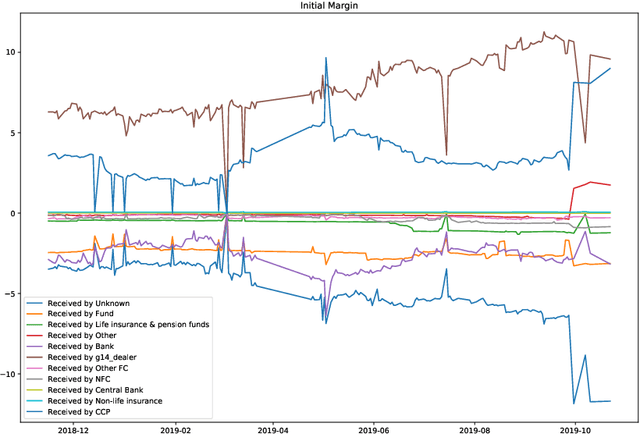
We study two questions related to competition on the OTC CDS market using data collected as part of the EMIR regulation. First, we study the competition between central counterparties through collateral requirements. We present models that successfully estimate the initial margin requirements. However, our estimations are not precise enough to use them as input to a predictive model for CCP choice by counterparties in the OTC market. Second, we model counterpart choice on the interdealer market using a novel semi-supervised predictive task. We present our methodology as part of the literature on model interpretability before arguing for the use of conditional entropy as the metric of interest to derive knowledge from data through a model-agnostic approach. In particular, we justify the use of deep neural networks to measure conditional entropy on real-world datasets. We create the $\textit{Razor entropy}$ using the framework of algorithmic information theory and derive an explicit formula that is identical to our semi-supervised training objective. Finally, we borrow concepts from game theory to define $\textit{top-k Shapley values}$. This novel method of payoff distribution satisfies most of the properties of Shapley values, and is of particular interest when the value function is monotone submodular. Unlike classical Shapley values, top-k Shapley values can be computed in quadratic time of the number of features instead of exponential. We implement our methodology and report the results on our particular task of counterpart choice. Finally, we present an improvement to the $\textit{node2vec}$ algorithm that could for example be used to further study intermediation. We show that the neighbor sampling used in the generation of biased walks can be performed in logarithmic time with a quasilinear time pre-computation, unlike the current implementations that do not scale well.