Competing Mutual Information Constraints with Stochastic Competition-based Activations for Learning Diversified Representations
Paper and Code
Jan 10, 2022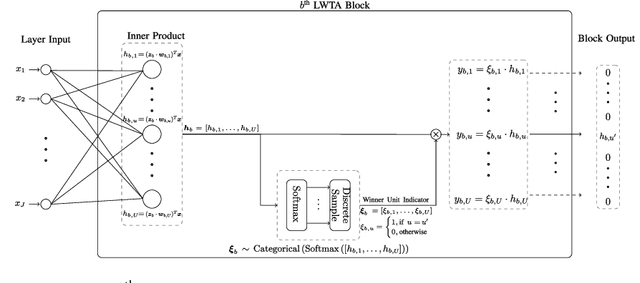
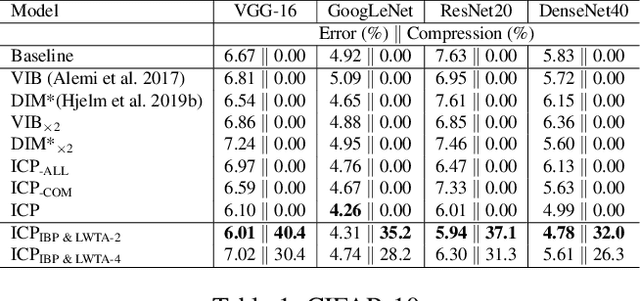
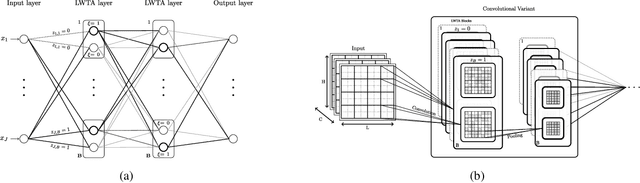
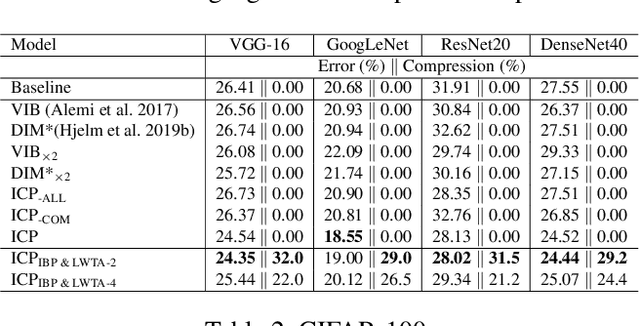
This work aims to address the long-established problem of learning diversified representations. To this end, we combine information-theoretic arguments with stochastic competition-based activations, namely Stochastic Local Winner-Takes-All (LWTA) units. In this context, we ditch the conventional deep architectures commonly used in Representation Learning, that rely on non-linear activations; instead, we replace them with sets of locally and stochastically competing linear units. In this setting, each network layer yields sparse outputs, determined by the outcome of the competition between units that are organized into blocks of competitors. We adopt stochastic arguments for the competition mechanism, which perform posterior sampling to determine the winner of each block. We further endow the considered networks with the ability to infer the sub-part of the network that is essential for modeling the data at hand; we impose appropriate stick-breaking priors to this end. To further enrich the information of the emerging representations, we resort to information-theoretic principles, namely the Information Competing Process (ICP). Then, all the components are tied together under the stochastic Variational Bayes framework for inference. We perform a thorough experimental investigation for our approach using benchmark datasets on image classification. As we experimentally show, the resulting networks yield significant discriminative representation learning abilities. In addition, the introduced paradigm allows for a principled investigation mechanism of the emerging intermediate network representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge