Combining Minkowski and Chebyshev: New distance proposal and survey of distance metrics using k-nearest neighbours classifier
Paper and Code
Dec 21, 2021
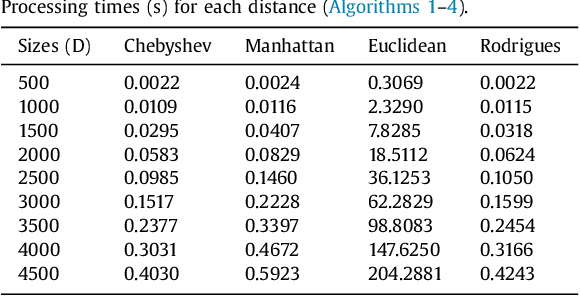
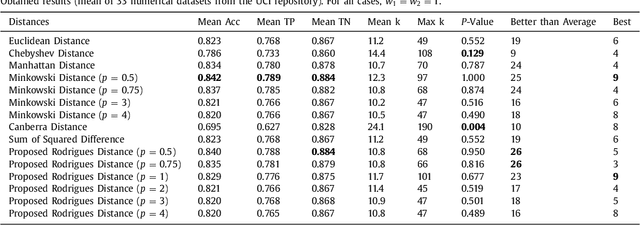
This work proposes a distance that combines Minkowski and Chebyshev distances and can be seen as an intermediary distance. This combination not only achieves efficient run times in neighbourhood iteration tasks in Z^2, but also obtains good accuracies when coupled with the k-Nearest Neighbours (k-NN) classifier. The proposed distance is approximately 1.3 times faster than Manhattan distance and 329.5 times faster than Euclidean distance in discrete neighbourhood iterations. An accuracy analysis of the k-NN classifier using a total of 33 datasets from the UCI repository, 15 distances and values assigned to k that vary from 1 to 200 is presented. In this experiment, the proposed distance obtained accuracies that were better than the average more often than its counterparts (in 26 cases out of 33), and also obtained the best accuracy more frequently (in 9 out of 33 cases).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge