Clustering by compression
Paper and Code
Apr 09, 2004
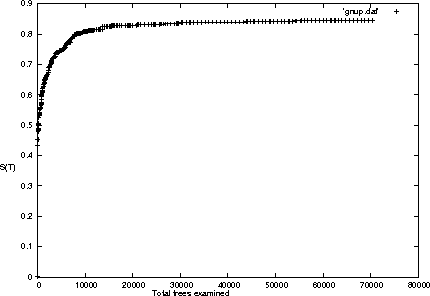
We present a new method for clustering based on compression. The method doesn't use subject-specific features or background knowledge, and works as follows: First, we determine a universal similarity distance, the normalized compression distance or NCD, computed from the lengths of compressed data files (singly and in pairwise concatenation). Second, we apply a hierarchical clustering method. The NCD is universal in that it is not restricted to a specific application area, and works across application area boundaries. A theoretical precursor, the normalized information distance, co-developed by one of the authors, is provably optimal but uses the non-computable notion of Kolmogorov complexity. We propose precise notions of similarity metric, normal compressor, and show that the NCD based on a normal compressor is a similarity metric that approximates universality. To extract a hierarchy of clusters from the distance matrix, we determine a dendrogram (binary tree) by a new quartet method and a fast heuristic to implement it. The method is implemented and available as public software, and is robust under choice of different compressors. To substantiate our claims of universality and robustness, we report evidence of successful application in areas as diverse as genomics, virology, languages, literature, music, handwritten digits, astronomy, and combinations of objects from completely different domains, using statistical, dictionary, and block sorting compressors. In genomics we presented new evidence for major questions in Mammalian evolution, based on whole-mitochondrial genomic analysis: the Eutherian orders and the Marsupionta hypothesis against the Theria hypothesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge