Clubs-based Particle Swarm Optimization
Paper and Code
Mar 02, 2013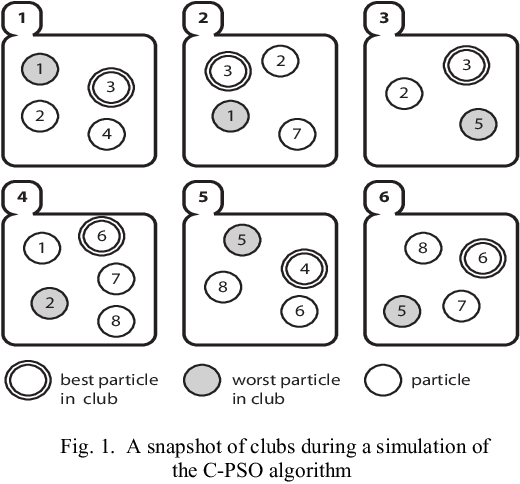

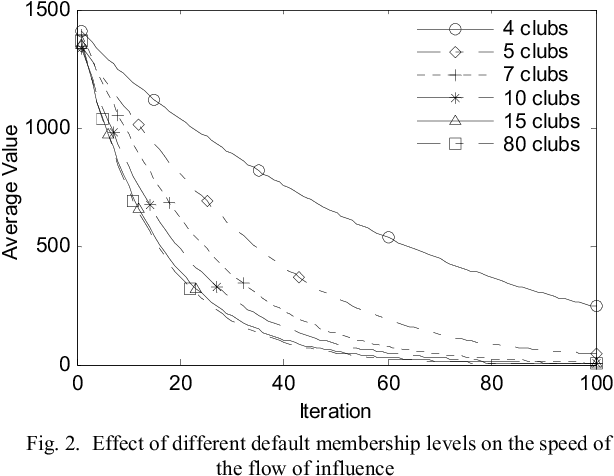
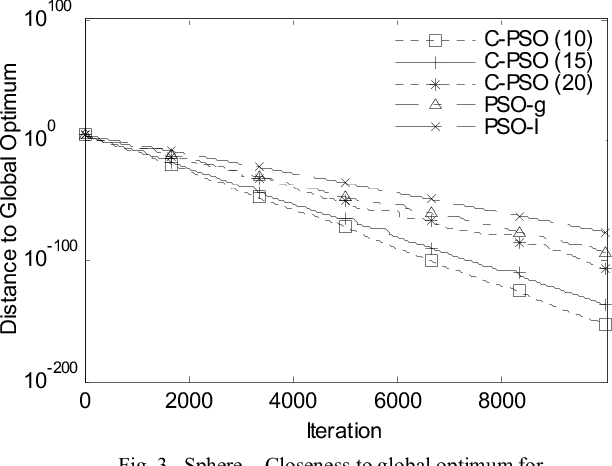
This paper introduces a new dynamic neighborhood network for particle swarm optimization. In the proposed Clubs-based Particle Swarm Optimization (C-PSO) algorithm, each particle initially joins a default number of what we call 'clubs'. Each particle is affected by its own experience and the experience of the best performing member of the clubs it is a member of. Clubs membership is dynamic, where the worst performing particles socialize more by joining more clubs to learn from other particles and the best performing particles are made to socialize less by leaving clubs to reduce their strong influence on other members. Particles return gradually to default membership level when they stop showing extreme performance. Inertia weights of swarm members are made random within a predefined range. This proposed dynamic neighborhood algorithm is compared with other two algorithms having static neighborhood topologies on a set of classic benchmark problems. The results showed superior performance for C-PSO regarding escaping local optima and convergence speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge