Channel Estimation for Beyond Diagonal RIS via Tensor Decomposition
Paper and Code
Jul 29, 2024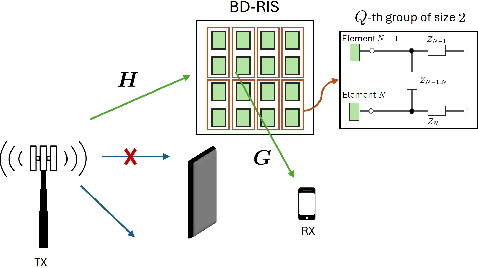
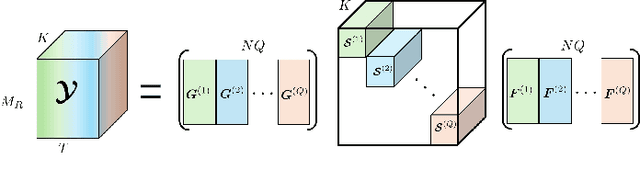
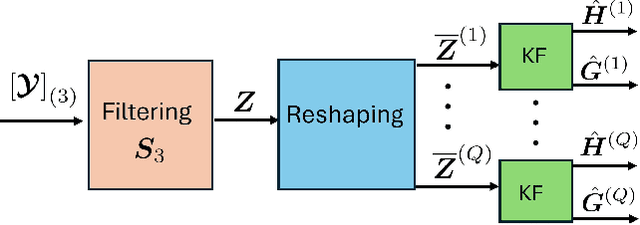
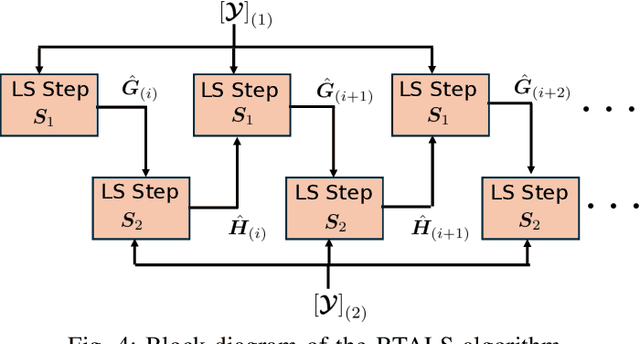
This paper addresses the channel estimation problem for beyond diagonal reconfigurable intelligent surface (BD-RIS) from a tensor decomposition perspective. We first show that the received pilot signals can be arranged as a three-way tensor, allowing us to recast the cascaded channel estimation problem as a block Tucker decomposition problem that yields decoupled estimates for the involved channel matrices while offering a substantial performance gain over the conventional (matrix-based) least squares (LS) estimation method. More specifically, we develop two solutions to solve the problem. The first one is a closed-form solution that extracts the channel estimates via a block Tucker Kronecker factorization (BTKF), which boils down to solving a set of parallel rank-one matrix approximation problems. Exploiting such a low-rank property yields a noise rejection gain compared to the standard LS estimation scheme while allowing the two involved channels to be estimated separately. The second solution is based on a block Tucker alternating least squares (BTALS) algorithm that directly estimates the involved channel matrices using an iterative estimation procedure. We discuss the uniqueness and identifiability issues and their implications for training design. We also propose a tensor-based design of the BD-RIS training tensor for each algorithm that ensures unique decoupled channel estimates under trivial scaling ambiguities. Our numerical results shed light on the tradeoffs offered by BTKF and BTALS methods. Specifically, while the first enjoys fast and parallel extraction of the channel estimates in closed form, the second has a more flexible training design, allowing for a significantly reduced training overhead compared to the state-of-the-art LS method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge