Causal Compression

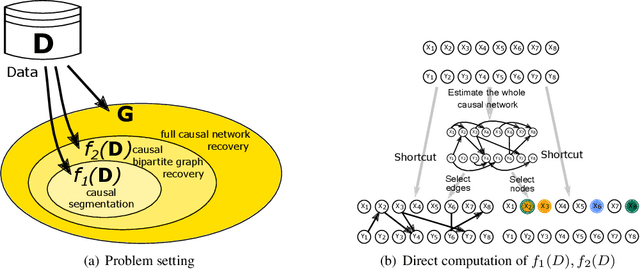
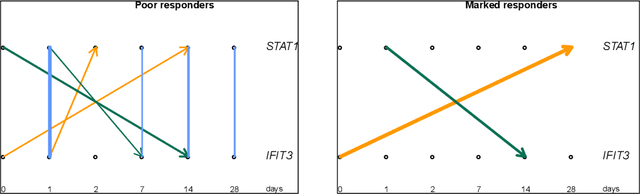
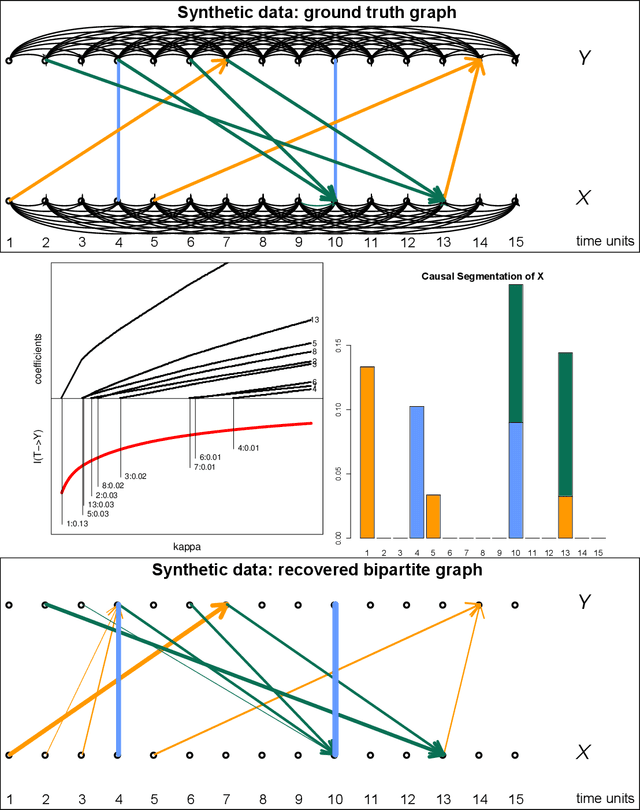
We propose a new method of discovering causal relationships in temporal data based on the notion of causal compression. To this end, we adopt the Pearlian graph setting and the directed information as an information theoretic tool for quantifying causality. We introduce chain rule for directed information and use it to motivate causal sparsity. We show two applications of the proposed method: causal time series segmentation which selects time points capturing the incoming and outgoing causal flow between time points belonging to different signals, and causal bipartite graph recovery. We prove that modelling of causality in the adopted set-up only requires estimating the copula density of the data distribution and thus does not depend on its marginals. We evaluate the method on time resolved gene expression data.