Canonical dual solutions to nonconvex radial basis neural network optimization problem
Paper and Code
Feb 18, 2013
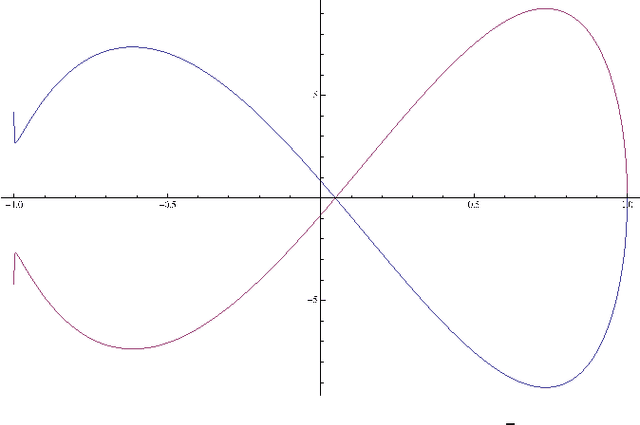
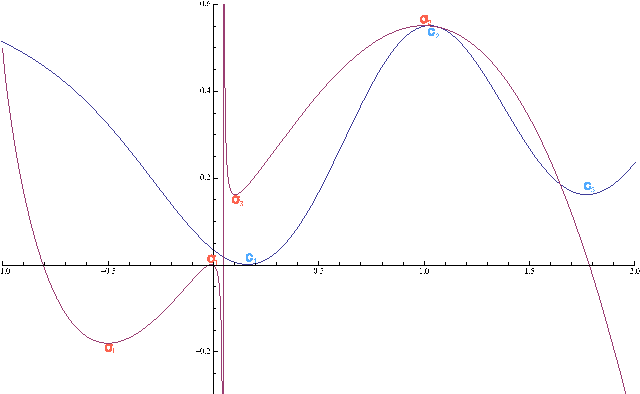
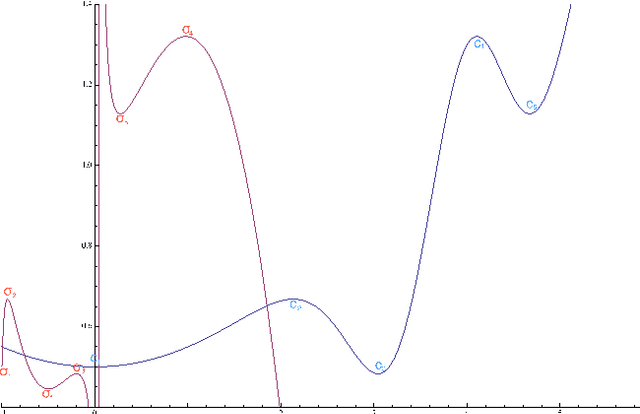
Radial Basis Functions Neural Networks (RBFNNs) are tools widely used in regression problems. One of their principal drawbacks is that the formulation corresponding to the training with the supervision of both the centers and the weights is a highly non-convex optimization problem, which leads to some fundamentally difficulties for traditional optimization theory and methods. This paper presents a generalized canonical duality theory for solving this challenging problem. We demonstrate that by sequential canonical dual transformations, the nonconvex optimization problem of the RBFNN can be reformulated as a canonical dual problem (without duality gap). Both global optimal solution and local extrema can be classified. Several applications to one of the most used Radial Basis Functions, the Gaussian function, are illustrated. Our results show that even for one-dimensional case, the global minimizer of the nonconvex problem may not be the best solution to the RBFNNs, and the canonical dual theory is a promising tool for solving general neural networks training problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge