Calibration of Derivative Pricing Models: a Multi-Agent Reinforcement Learning Perspective

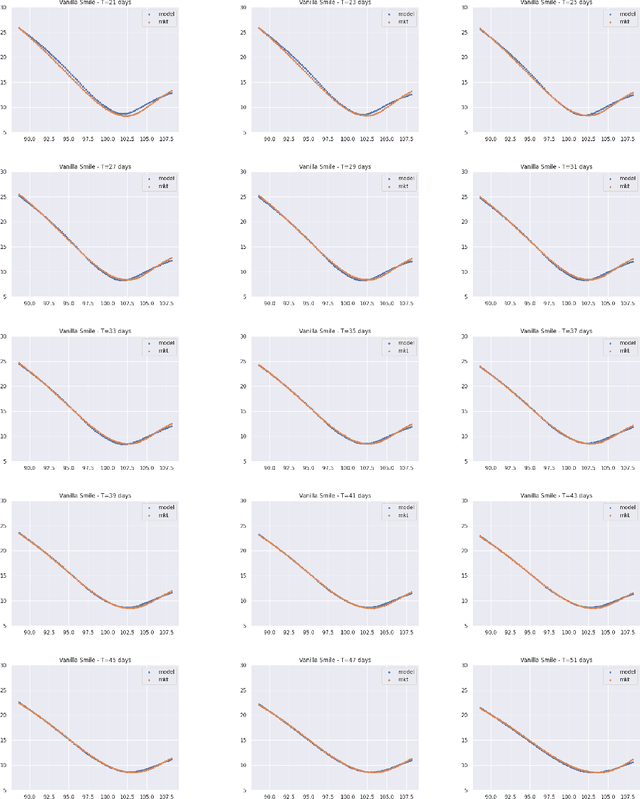
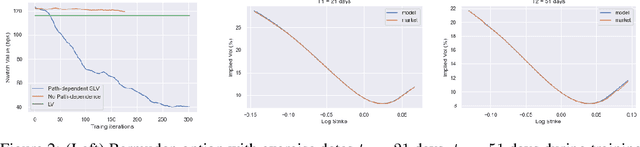
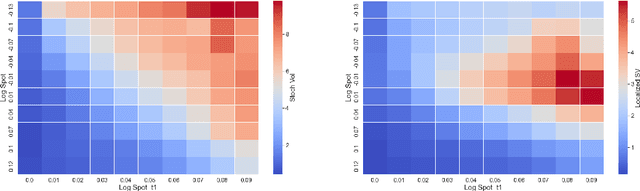
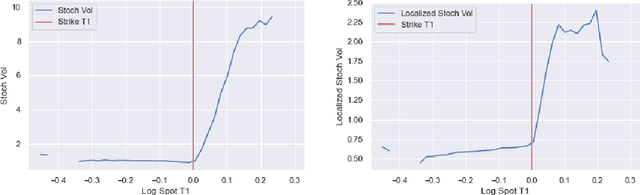
One of the most fundamental questions in quantitative finance is the existence of continuous-time diffusion models that fit market prices of a given set of options. Traditionally, one employs a mix of intuition, theoretical and empirical analysis to find models that achieve exact or approximate fits. Our contribution is to show how a suitable game theoretical formulation of this problem can help solve this question by leveraging existing developments in modern deep multi-agent reinforcement learning to search in the space of stochastic processes. More importantly, we hope that our techniques can be leveraged and extended by the community to solve important problems in that field, such as the joint SPX-VIX calibration problem. Our experiments show that we are able to learn local volatility, as well as path-dependence required in the volatility process to minimize the price of a Bermudan option. In one sentence, our algorithm can be seen as a particle method \`{a} la Guyon et Henry-Labordere where particles, instead of being designed to ensure $\sigma_{loc}(t,S_t)^2 = \mathbb{E}[\sigma_t^2|S_t]$, are learning RL-driven agents cooperating towards more general calibration targets. This is the first work bridging reinforcement learning with the derivative calibration problem.