Calibration by Distribution Matching: Trainable Kernel Calibration Metrics
Paper and Code
Oct 31, 2023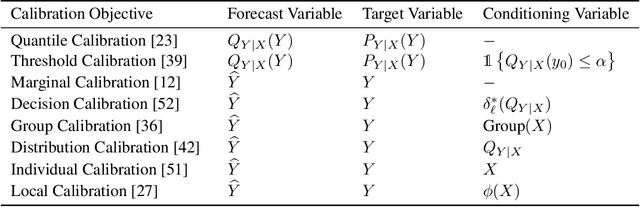
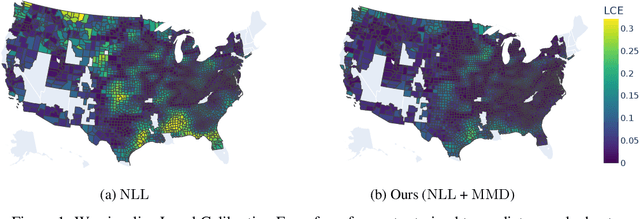

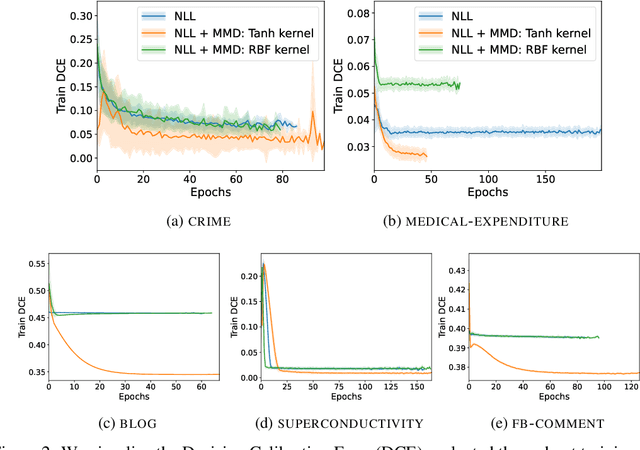
Calibration ensures that probabilistic forecasts meaningfully capture uncertainty by requiring that predicted probabilities align with empirical frequencies. However, many existing calibration methods are specialized for post-hoc recalibration, which can worsen the sharpness of forecasts. Drawing on the insight that calibration can be viewed as a distribution matching task, we introduce kernel-based calibration metrics that unify and generalize popular forms of calibration for both classification and regression. These metrics admit differentiable sample estimates, making it easy to incorporate a calibration objective into empirical risk minimization. Furthermore, we provide intuitive mechanisms to tailor calibration metrics to a decision task, and enforce accurate loss estimation and no regret decisions. Our empirical evaluation demonstrates that employing these metrics as regularizers enhances calibration, sharpness, and decision-making across a range of regression and classification tasks, outperforming methods relying solely on post-hoc recalibration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge