Bounding the expectation of the supremum of empirical processes indexed by Hölder classes
Paper and Code
Mar 30, 2020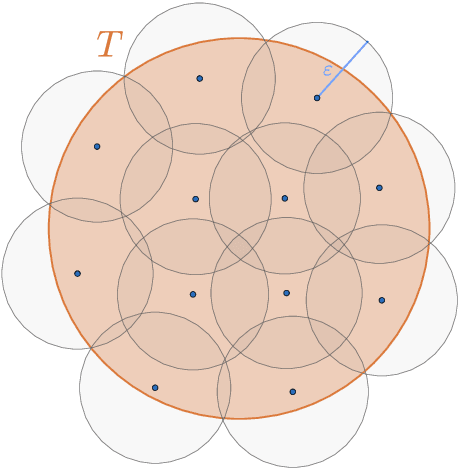
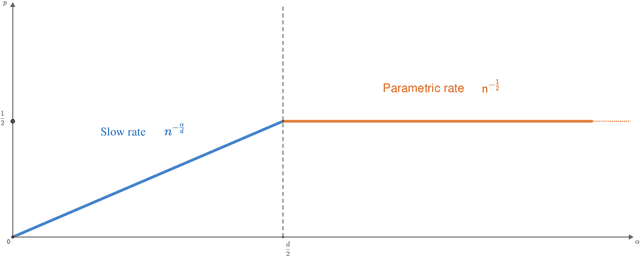
We obtain upper bounds on the expectation of the supremum of empirical processes indexed by H\"older classes of any smoothness and for any distribution supported on a bounded set. Another way to see it is from the point of view of integral probability metrics (IPM), a class of metrics on the space of probability measures: our rates quantify how quickly the empirical measure obtained from $n$ independent samples from a probability measure $P$ approaches $P$ with respect to the IPM indexed by H\"older classes. As an extremal case we recover the known rates for the Wassertein-1 distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge