Bipartite Matchings with Group Fairness and Individual Fairness Constraints
Paper and Code
Aug 23, 2022
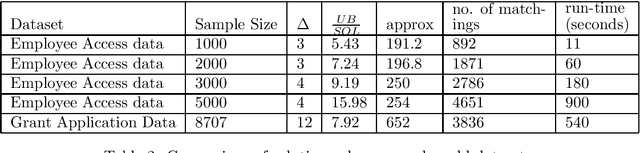
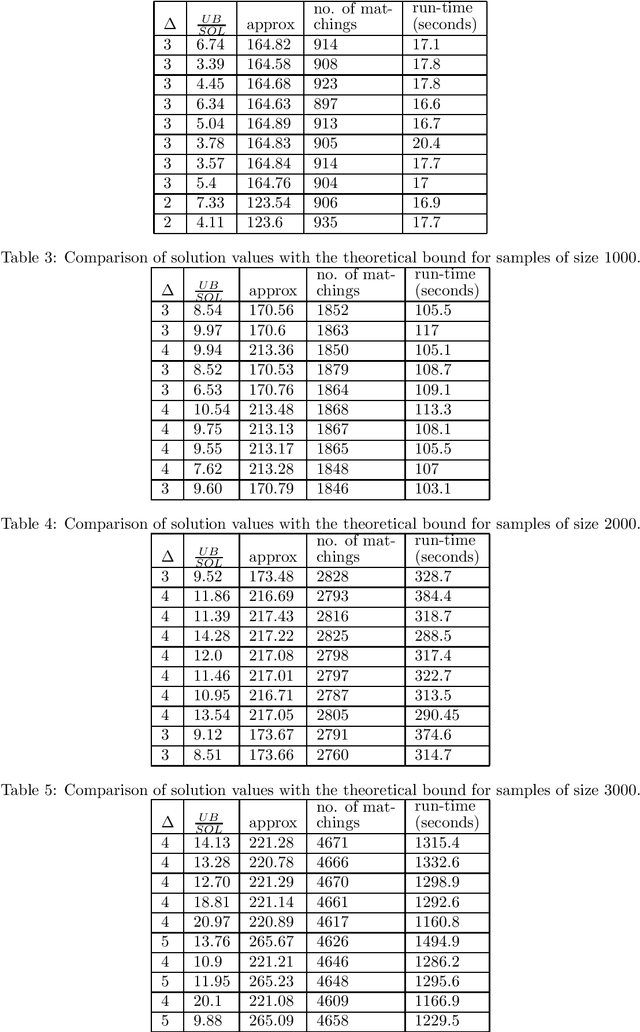
We address group as well as individual fairness constraints in matchings in the context of assigning items to platforms. Each item belongs to certain groups and has a preference ordering over platforms. Each platform enforces group fairness by specifying an upper and a lower bound on the number of items that can be matched to it from each group. There could be multiple optimal solutions that satisfy the group fairness constraints. To achieve individual fairness, we introduce `probabilistic individual fairness', where the goal is to compute a distribution over `group fair' matchings such that every item has a reasonable probability of being matched to a platform among its top choices. In the case where each item belongs to exactly one group, we provide a polynomial-time algorithm that computes a probabilistic individually fair distribution over group fair matchings. When an item can belong to multiple groups, and the group fairness constraints are specified as only upper bounds, we rehash the same algorithm to achieve three different polynomial-time approximation algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge