Binary Search and First Order Gradient Based Method for Stochastic Optimization

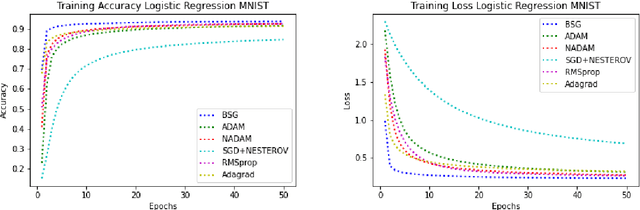
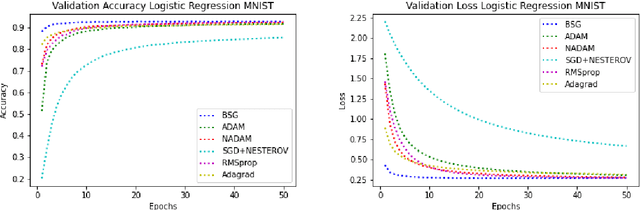
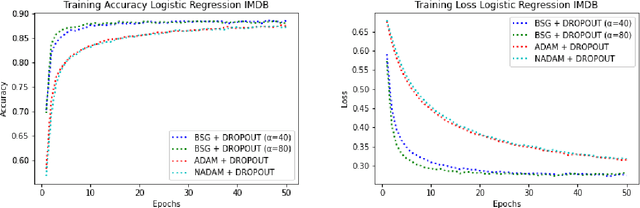
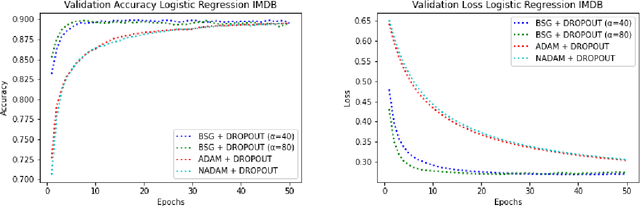
In this paper, we present a novel stochastic optimization method, which uses the binary search technique with first order gradient based optimization method, called Binary Search Gradient Optimization (BSG) or BiGrad. In this optimization setup, a non-convex surface is treated as a set of convex surfaces. In BSG, at first, a region is defined, assuming region is convex. If region is not convex, then the algorithm leaves the region very fast and defines a new one, otherwise, it tries to converge at the optimal point of the region. In BSG, core purpose of binary search is to decide, whether region is convex or not in logarithmic time, whereas, first order gradient based method is primarily applied, to define a new region. In this paper, Adam is used as a first order gradient based method, nevertheless, other methods of this class may also be considered. In deep neural network setup, it handles the problem of vanishing and exploding gradient efficiently. We evaluate BSG on the MNIST handwritten digit, IMDB, and CIFAR10 data set, using logistic regression and deep neural networks. We produce more promising results as compared to other first order gradient based optimization methods. Furthermore, proposed algorithm generalizes significantly better on unseen data as compared to other methods.