Bayesian Neural Networks
Paper and Code
Jan 30, 2018
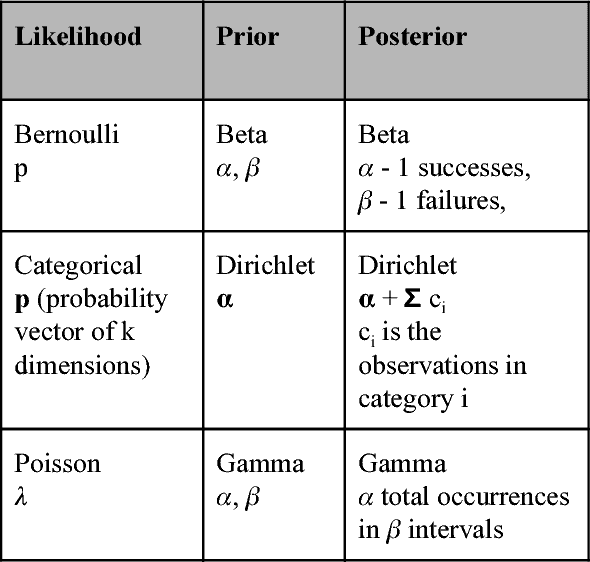
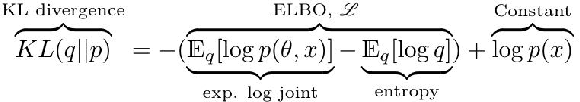
This paper describes and discusses Bayesian Neural Network (BNN). The paper showcases a few different applications of them for classification and regression problems. BNNs are comprised of a Probabilistic Model and a Neural Network. The intent of such a design is to combine the strengths of Neural Networks and Stochastic modeling. Neural Networks exhibit continuous function approximator capabilities. Stochastic models allow direct specification of a model with known interaction between parameters to generate data. During the prediction phase, stochastic models generate a complete posterior distribution and produce probabilistic guarantees on the predictions. Thus BNNs are a unique combination of neural network and stochastic models with the stochastic model forming the core of this integration. BNNs can then produce probabilistic guarantees on it's predictions and also generate the distribution of parameters that it has learnt from the observations. That means, in the parameter space, one can deduce the nature and shape of the neural network's learnt parameters. These two characteristics makes them highly attractive to theoreticians as well as practitioners. Recently there has been a lot of activity in this area, with the advent of numerous probabilistic programming libraries such as: PyMC3, Edward, Stan etc. Further this area is rapidly gaining ground as a standard machine learning approach for numerous problems
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge