Bayesian Assessment of a Connectionist Model for Fault Detection
Paper and Code
Mar 27, 2013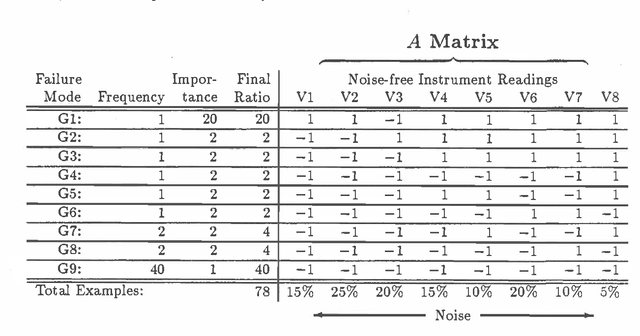
A previous paper [2] showed how to generate a linear discriminant network (LDN) that computes likely faults for a noisy fault detection problem by using a modification of the perceptron learning algorithm called the pocket algorithm. Here we compare the performance of this connectionist model with performance of the optimal Bayesian decision rule for the example that was previously described. We find that for this particular problem the connectionist model performs about 97% as well as the optimal Bayesian procedure. We then define a more general class of noisy single-pattern boolean (NSB) fault detection problems where each fault corresponds to a single :pattern of boolean instrument readings and instruments are independently noisy. This is equivalent to specifying that instrument readings are probabilistic but conditionally independent given any particular fault. We prove: 1. The optimal Bayesian decision rule for every NSB fault detection problem is representable by an LDN containing no intermediate nodes. (This slightly extends a result first published by Minsky & Selfridge.) 2. Given an NSB fault detection problem, then with arbitrarily high probability after sufficient iterations the pocket algorithm will generate an LDN that computes an optimal Bayesian decision rule for that problem. In practice we find that a reasonable number of iterations of the pocket algorithm produces a network with good, but not optimal, performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge