Bandits Corrupted by Nature: Lower Bounds on Regret and Robust Optimistic Algorithm
Paper and Code
Mar 07, 2022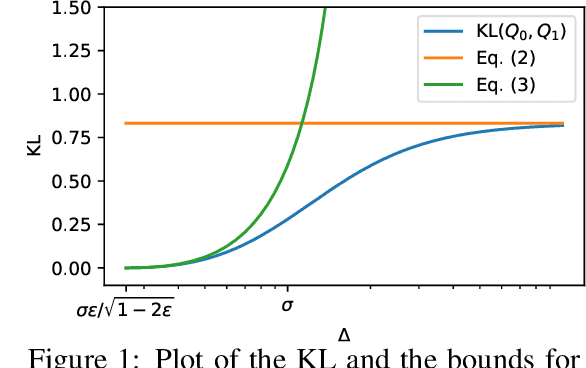
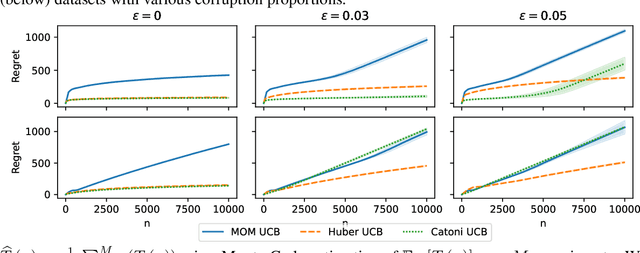
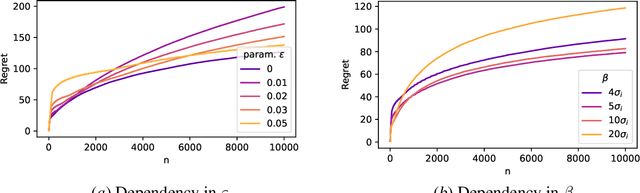
In this paper, we study the stochastic bandits problem with $k$ unknown heavy-tailed and corrupted reward distributions or arms with time-invariant corruption distributions. At each iteration, the player chooses an arm. Given the arm, the environment returns an uncorrupted reward with probability $1-\varepsilon$ and an arbitrarily corrupted reward with probability $\varepsilon$. In our setting, the uncorrupted reward might be heavy-tailed and the corrupted reward might be unbounded. We prove a lower bound on the regret indicating that the corrupted and heavy-tailed bandits are strictly harder than uncorrupted or light-tailed bandits. We observe that the environments can be categorised into hardness regimes depending on the suboptimality gap $\Delta$, variance $\sigma$, and corruption proportion $\epsilon$. Following this, we design a UCB-type algorithm, namely HuberUCB, that leverages Huber's estimator for robust mean estimation. HuberUCB leads to tight upper bounds on regret in the proposed corrupted and heavy-tailed setting. To derive the upper bound, we prove a novel concentration inequality for Huber's estimator, which might be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge