Approximation of Reeb spaces with Mappers and Applications to Stochastic Filters
Paper and Code
Dec 23, 2019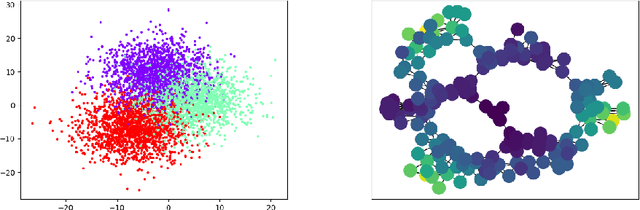
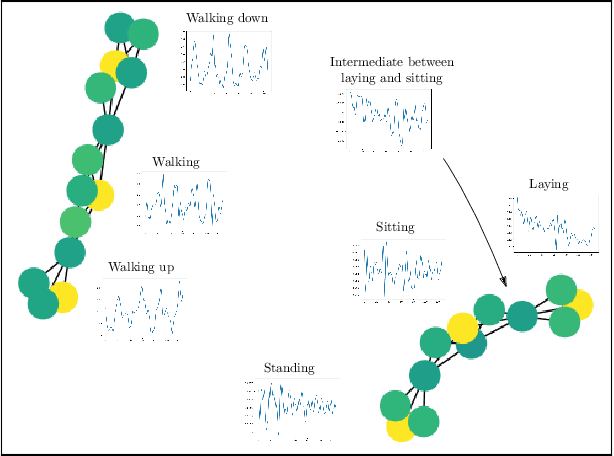
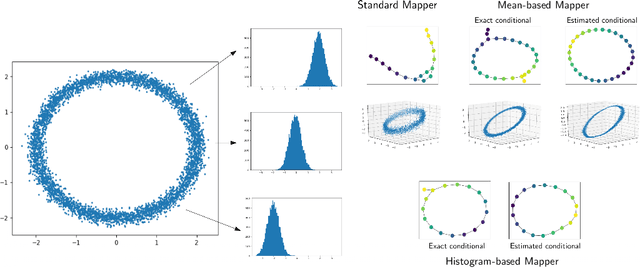
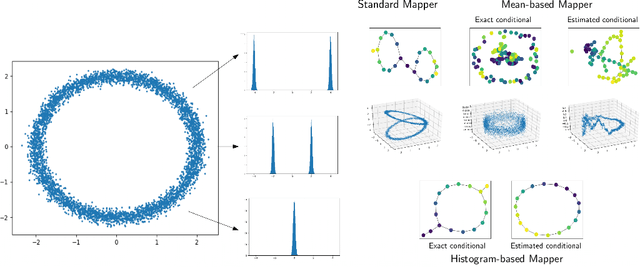
Reeb spaces, as well as their discretized versions called Mappers, are common descriptors used in Topological Data Analysis, with plenty of applications in various fields of science, such as computational biology and data visualization, among others. The stability and quantification of the rate of convergence of the Mapper to the Reeb space has been studied a lot in recent works~\cite{Brown2019, Carriere2018a, Carriere2018, Munch2016}, focusing on the case where a scalar-valued filter is used for the computation of Mapper. On the other hand, much less is known in the multivariate case, where the domain of the filter is in $\mathbb R^d$ instead of $\mathbb R$. The only available result in this setting~\cite{Munch2016} only works for topological spaces and cannot be used as is for finite metric spaces representing data, such as point clouds and distance matrices. In this article, we present an approximation result for the Reeb space in the multivariate case using a Mapper-based estimator, which is a slight modification of the usual Mapper construction. Moreover, our approximation is stated with respect to a pseudometric that is an extension of the usual {\em interleaving distance} between persistence modules~\cite{Chazal2016}. Finally, we apply our results to the case where the filter function used to compute the Mapper is estimated from the data. We provide applications of this setting in statistics and machine learning and probability for different kinds of target filters, as well as numerical experiments that demonstrate the relevance of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge