Approximation learning methods of Harmonic Mappings in relation to Hardy Spaces

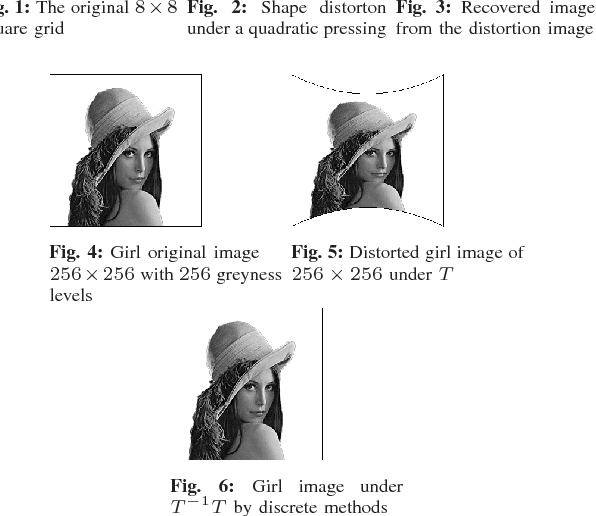
A new Hardy space Hardy space approach of Dirichlet type problem based on Tikhonov regularization and Reproducing Hilbert kernel space is discussed in this paper, which turns out to be a typical extremal problem located on the upper upper-high complex plane. If considering this in the Hardy space, the optimization operator of this problem will be highly simplified and an efficient algorithm is possible. This is mainly realized by the help of reproducing properties of the functions in the Hardy space of upper-high complex plane, and the detail algorithm is proposed. Moreover, harmonic mappings, which is a significant geometric transformation, are commonly used in many applications such as image processing, since it describes the energy minimization mappings between individual manifolds. Particularly, when we focus on the planer mappings between two Euclid planer regions, the harmonic mappings are exist and unique, which is guaranteed solidly by the existence of harmonic function. This property is attractive and simulation results are shown in this paper to ensure the capability of applications such as planer shape distortion and surface registration.