Analyzing Modularity Maximization in Approximation, Heuristic, and Graph Neural Network Algorithms for Community Detection

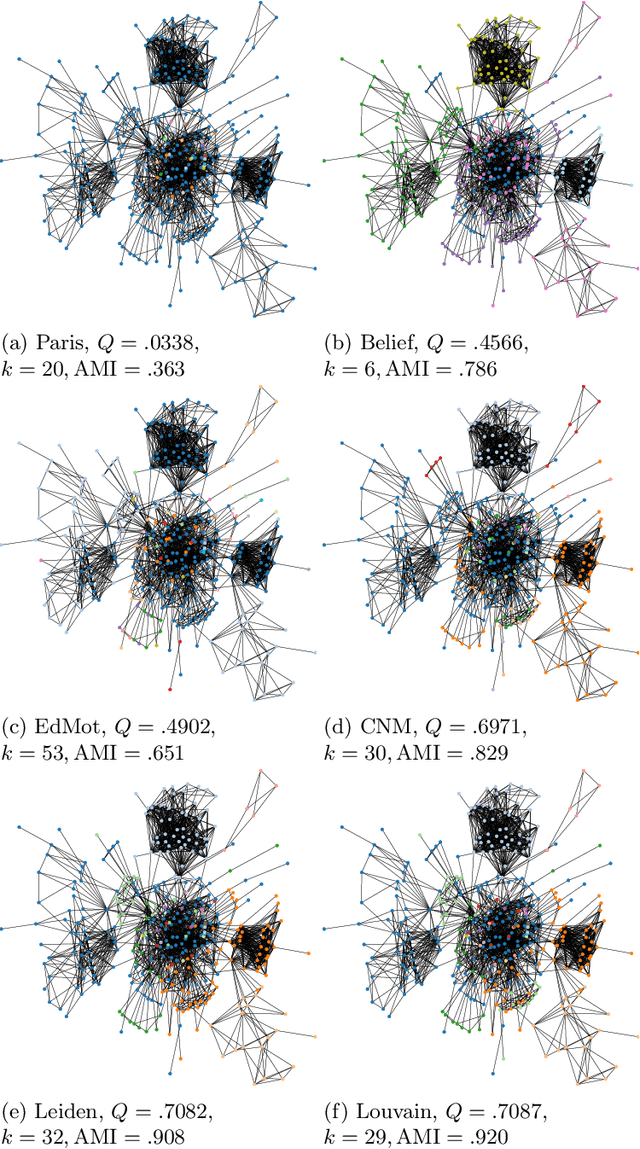
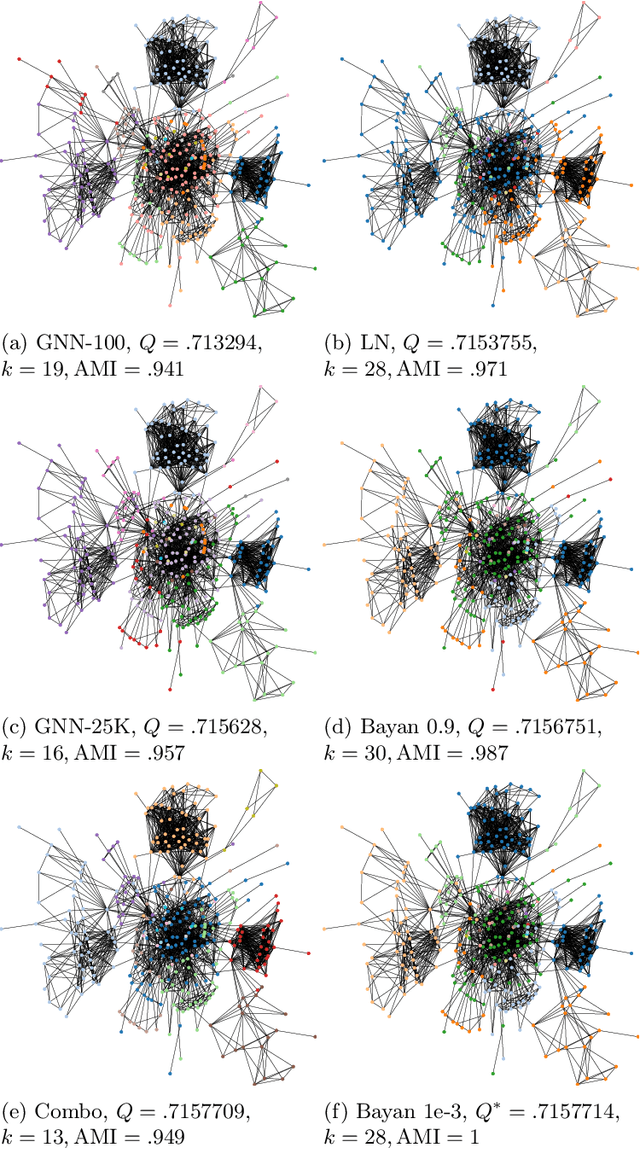
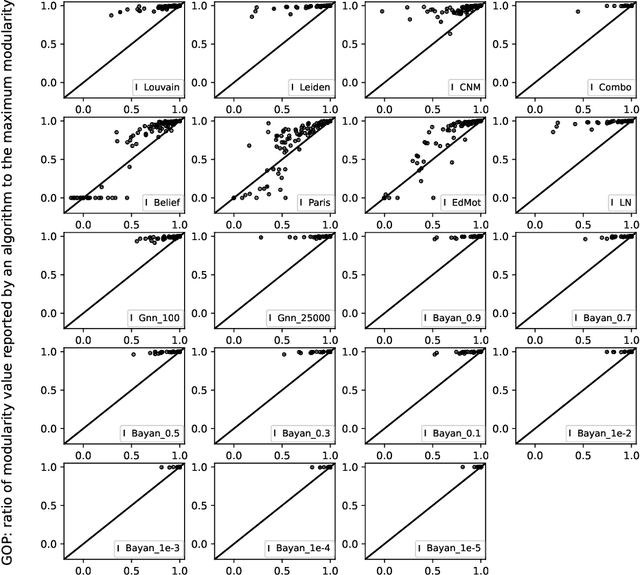
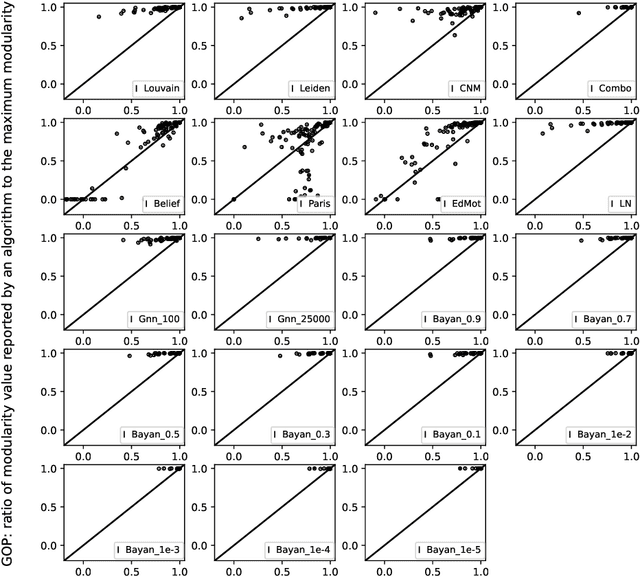
Community detection, a fundamental problem in computational sciences, finds applications in various domains. Heuristics are often employed to detect communities through maximizing an objective function, modularity, over partitions of network nodes. Our research delves into the performance of different modularity maximization algorithms in achieving optimal partitions. We use 104 networks, comprising real-world instances from diverse contexts and synthetic graphs with modular structures. We analyze ten inexact modularity-based algorithms against an exact baseline which is an exact integer programming method that globally optimizes modularity. The ten algorithms analyzed include eight heuristics, two variations of a graph neural network algorithm, and several variations of the Bayan approximation algorithm. Our analysis uncovers substantial dissimilarities between the partitions obtained by most commonly used modularity-based methods and any optimal partition of the networks, as indicated by both adjusted and reduced mutual information metrics. Importantly, our results show that near-optimal partitions are often disproportionately dissimilar to any optimal partition. Taken together, our analysis points to a crucial limitation of the commonly used unguaranteed modularity-based methods for discovering communities: they rarely produce an optimal partition or a partition resembling an optimal partition even on networks with modular structures. If modularity is to be used for detecting communities, approximate optimization algorithms are recommendable for a more methodologically sound usage of modularity within its applicability limits.