Analytic Mutual Information in Bayesian Neural Networks
Paper and Code
Jan 24, 2022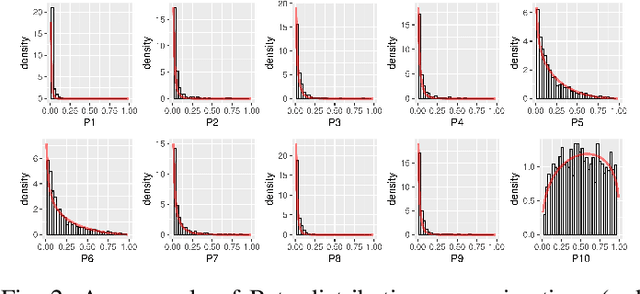
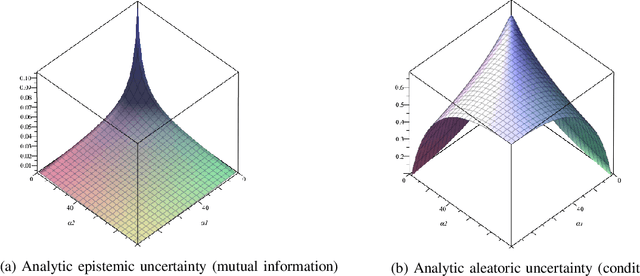
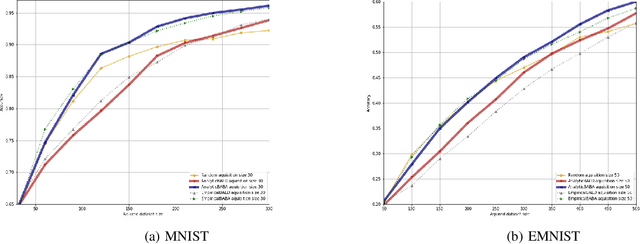
Bayesian neural networks have successfully designed and optimized a robust neural network model in many application problems, including uncertainty quantification. However, with its recent success, information-theoretic understanding about the Bayesian neural network is still at an early stage. Mutual information is an example of an uncertainty measure in a Bayesian neural network to quantify epistemic uncertainty. Still, no analytic formula is known to describe it, one of the fundamental information measures to understand the Bayesian deep learning framework. In this paper, with the Dirichlet distribution assumption in its intermediate encoded message, we derive the analytical formula of the mutual information between model parameters and the predictive output by leveraging the notion of the point process entropy. Then, as an application, we discuss the estimation of the Dirichlet parameters and show its practical application in the active learning uncertainty measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge