Analysis of a new chaotic system, electronic realization and use in navigation of differential drive mobile robot
Paper and Code
Dec 11, 2020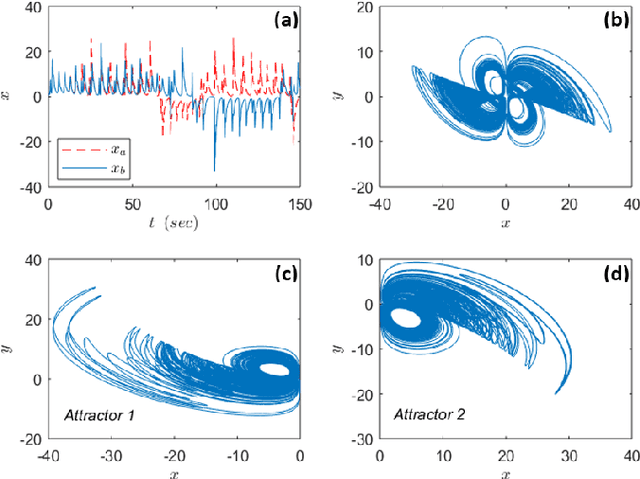
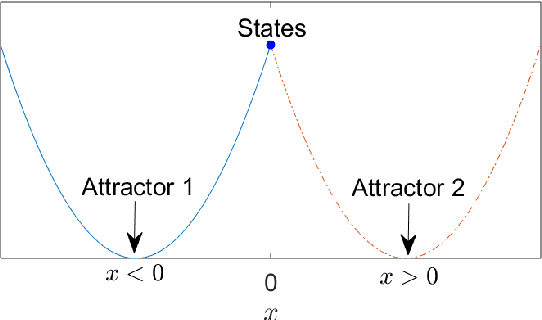
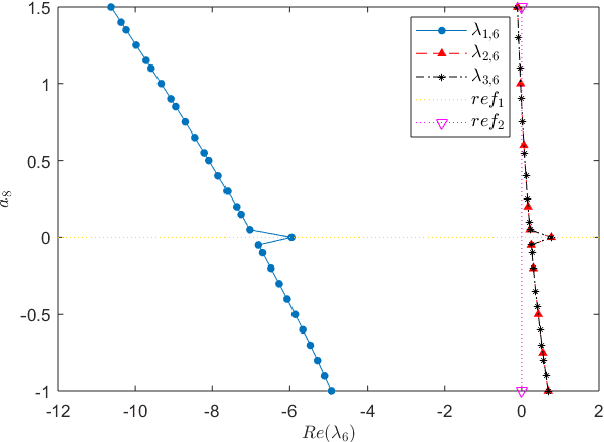
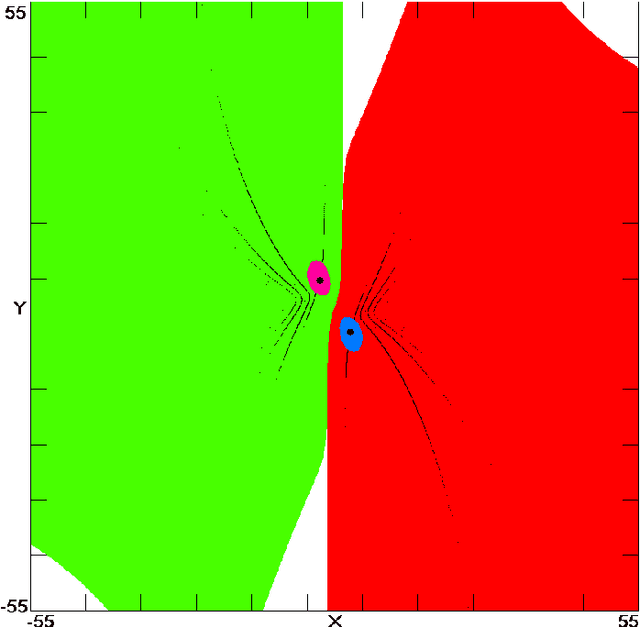
This paper presents a new chaotic system having four attractors, including two fixed point attractors and two symmetrical chaotic strange attractors. Dynamical properties of the system, viz. sensitive dependence on initial conditions, Lyapunov spectrum, strangeness measure, attraction basin, including the class and size of it, existence of strange attractor, bifurcation analysis, multistability, electronic circuit design, and hardware implementation, are rigorously treated. Numerical computations are used to compute the basin of attraction and show that the system has a far-reaching composite basin of attraction. Such a basin of attraction is vital for engineering applications. Moreover, a circuit model of the system is realized using analog electronic components. A procedure is detailed for converting the system parameters into corresponding electronic component values such as the circuital resistances while ensuring the dynamic ranges are bounded. Besides, the system is used as the source of control inputs for independent navigation of a differential drive mobile robot, which is subject to the Pfaffian velocity constraint. Due to the properties of sensitivity on initial conditions and topological mixing, the robot's path becomes unpredictable and guaranteed to scan the workspace, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge