An Optimal Algorithm for Adversarial Bandits with Arbitrary Delays
Paper and Code
Oct 14, 2019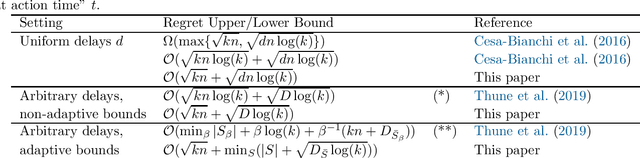

We propose a new algorithm for adversarial multi-armed bandits with unrestricted delays. The algorithm is based on a novel hybrid regularizer applied in the Follow the Regularized Leader (FTRL) framework. It achieves $\mathcal{O}(\sqrt{kn}+\sqrt{D\log(k)})$ regret guarantee, where $k$ is the number of arms, $n$ is the number of rounds, and $D$ is the total delay. The result matches the lower bound within constants and requires no prior knowledge of $n$ or $D$. Additionally, we propose a refined tuning of the algorithm, which achieves $\mathcal{O}(\sqrt{kn}+\min_{S}|S|+\sqrt{D_{\bar S}\log(k)})$ regret guarantee, where $S$ is a set of rounds excluded from delay counting, $\bar S = [n]\setminus S$ are the counted rounds, and $D_{\bar S}$ is the total delay in the counted rounds. If the delays are highly unbalanced, the latter regret guarantee can be significantly tighter than the former. The result requires no advance knowledge of the delays and resolves an open problem of Thune et al. (2019). The new FTRL algorithm and its refined tuning are anytime and require no doubling, which resolves another open problem of Thune et al. (2019).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge