An introduction to Topological Data Analysis: fundamental and practical aspects for data scientists

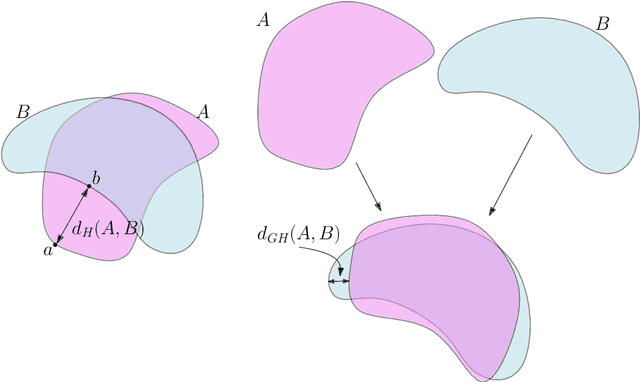
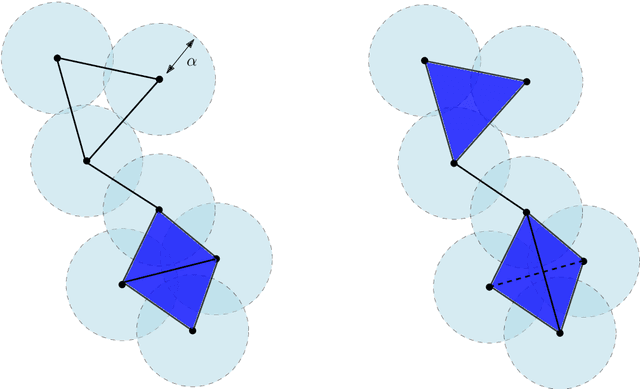
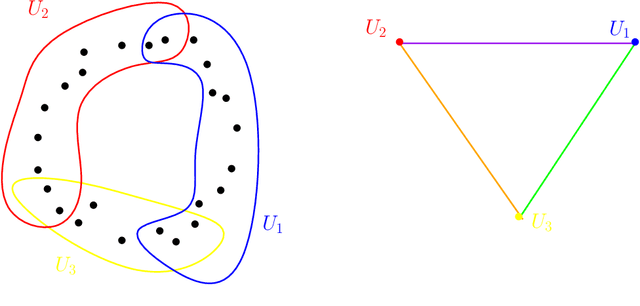
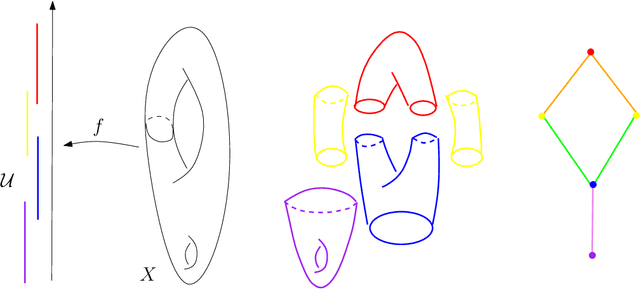
Topological Data Analysis (tda) is a recent and fast growing eld providing a set of new topological and geometric tools to infer relevant features for possibly complex data. This paper is a brief introduction, through a few selected topics, to basic fundamental and practical aspects of tda for non experts. 1 Introduction and motivation Topological Data Analysis (tda) is a recent eld that emerged from various works in applied (algebraic) topology and computational geometry during the rst decade of the century. Although one can trace back geometric approaches for data analysis quite far in the past, tda really started as a eld with the pioneering works of Edelsbrunner et al. (2002) and Zomorodian and Carlsson (2005) in persistent homology and was popularized in a landmark paper in 2009 Carlsson (2009). tda is mainly motivated by the idea that topology and geometry provide a powerful approach to infer robust qualitative, and sometimes quantitative, information about the structure of data-see, e.g. Chazal (2017). tda aims at providing well-founded mathematical, statistical and algorithmic methods to infer, analyze and exploit the complex topological and geometric structures underlying data that are often represented as point clouds in Euclidean or more general metric spaces. During the last few years, a considerable eort has been made to provide robust and ecient data structures and algorithms for tda that are now implemented and available and easy to use through standard libraries such as the Gudhi library (C++ and Python) Maria et al. (2014) and its R software interface Fasy et al. (2014a). Although it is still rapidly evolving, tda now provides a set of mature and ecient tools that can be used in combination or complementary to other data sciences tools. The tdapipeline. tda has recently known developments in various directions and application elds. There now exist a large variety of methods inspired by topological and geometric approaches. Providing a complete overview of all these existing approaches is beyond the scope of this introductory survey. However, most of them rely on the following basic and standard pipeline that will serve as the backbone of this paper: 1. The input is assumed to be a nite set of points coming with a notion of distance-or similarity between them. This distance can be induced by the metric in the ambient space (e.g. the Euclidean metric when the data are embedded in R d) or come as an intrinsic metric dened by a pairwise distance matrix. The denition of the metric on the data is usually given as an input or guided by the application. It is however important to notice that the choice of the metric may be critical to reveal interesting topological and geometric features of the data.