An Empirical Study of w-Cutset Sampling for Bayesian Networks
Paper and Code
Oct 19, 2012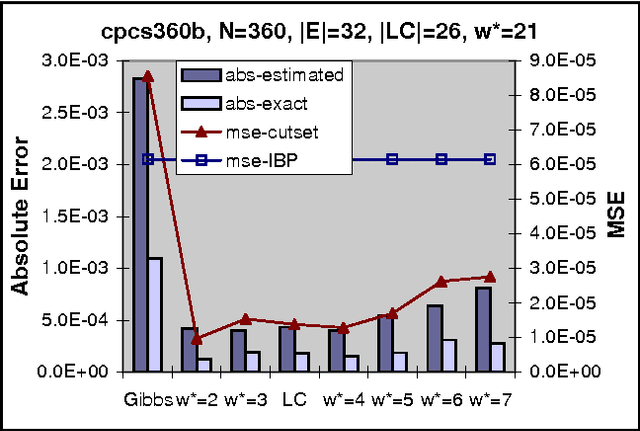
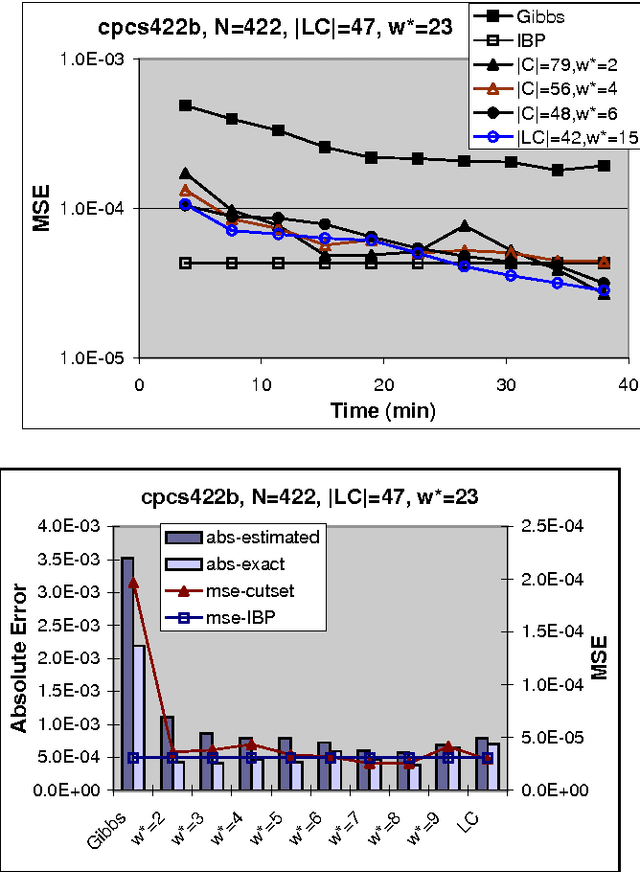
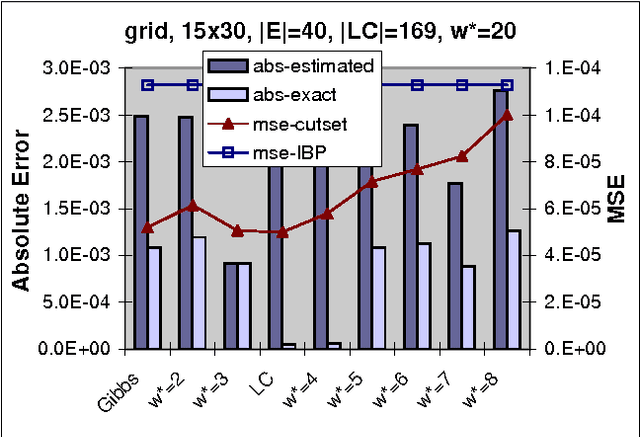
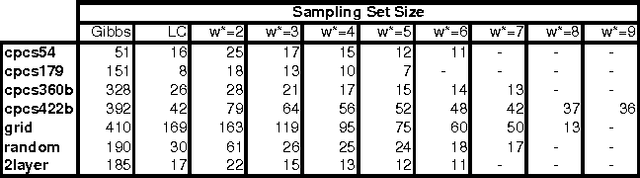
The paper studies empirically the time-space trade-off between sampling and inference in a sl cutset sampling algorithm. The algorithm samples over a subset of nodes in a Bayesian network and applies exact inference over the rest. Consequently, while the size of the sampling space decreases, requiring less samples for convergence, the time for generating each single sample increases. The w-cutset sampling selects a sampling set such that the induced-width of the network when the sampling set is observed is bounded by w, thus requiring inference whose complexity is exponential in w. In this paper, we investigate performance of w-cutset sampling over a range of w values and measure the accuracy of w-cutset sampling as a function of w. Our experiments demonstrate that the cutset sampling idea is quite powerful showing that an optimal balance between inference and sampling benefits substantially from restricting the cutset size, even at the cost of more complex inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge