An efficient feature-preserving PDE algorithm for image denoising based on a spatial-fractional anisotropic diffusion equation

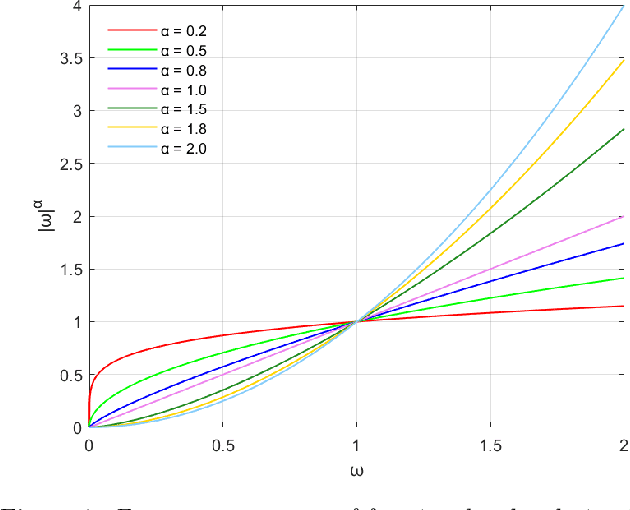
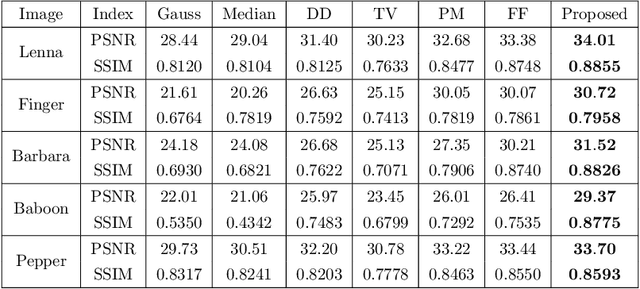
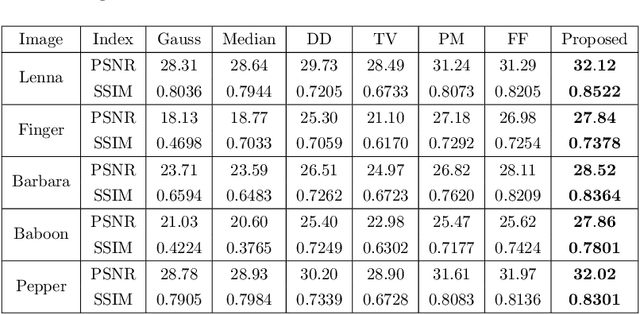
How to effectively remove the noise while preserving the image structure features is a challenging issue in the field of image denoising. In recent years, fractional PDE based methods have attracted more and more research efforts due to the ability to balance the noise removal and the preservation of image edges and textures. Among the existing fractional PDE algorithms, there are only a few using spatial fractional order derivatives, and all the fractional derivatives involved are one-sided derivatives. In this paper, an efficient feature-preserving fractional PDE algorithm is proposed for image denoising based on a nonlinear spatial-fractional anisotropic diffusion equation. Two-sided Grumwald-Letnikov fractional derivatives were used in the PDE model which are suitable to depict the local self-similarity of images. The Short Memory Principle is employed to simplify the approximation scheme. Experimental results show that the proposed method is of a satisfactory performance, i.e. it keeps a remarkable balance between noise removal and feature preserving, and has an extremely high structural retention property.