Adversarial Risk Bounds for Binary Classification via Function Transformation

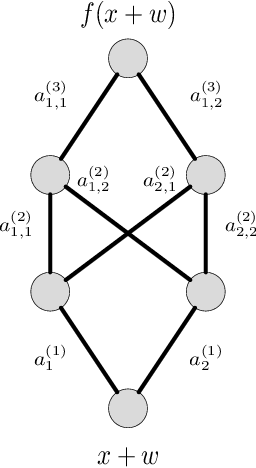
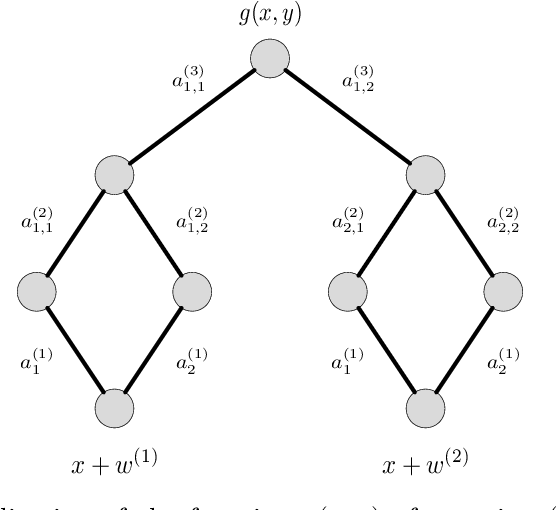
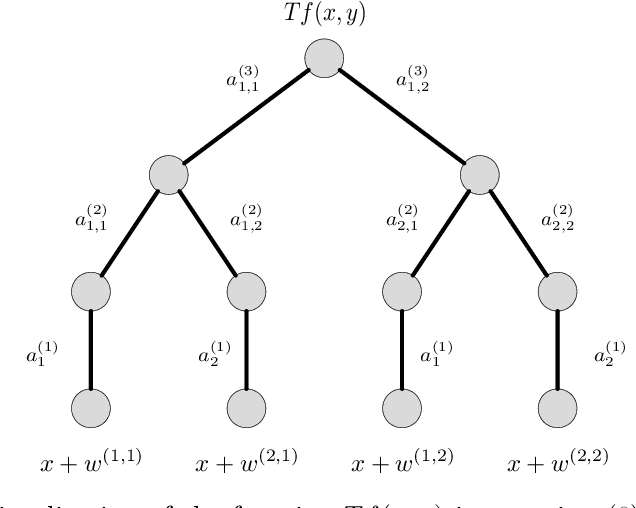
We derive new bounds for a notion of adversarial risk, characterizing the robustness of binary classifiers. Specifically, we study the cases of linear classifiers and neural network classifiers, and introduce transformations with the property that the risk of the transformed functions upper-bounds the adversarial risk of the original functions. This reduces the problem of deriving adversarial risk bounds to the problem of deriving risk bounds using standard learning-theoretic techniques. We then derive bounds on the Rademacher complexities of the transformed function classes, obtaining error rates on the same order as the generalization error of the original function classes. Finally, we provide two algorithms for optimizing the adversarial risk bounds in the linear case, and discuss connections to regularization and distributional robustness.