Adversarial contamination of networks in the setting of vertex nomination: a new trimming method
Paper and Code
Aug 20, 2022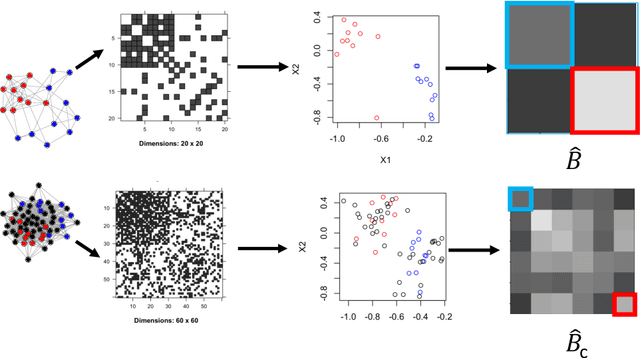
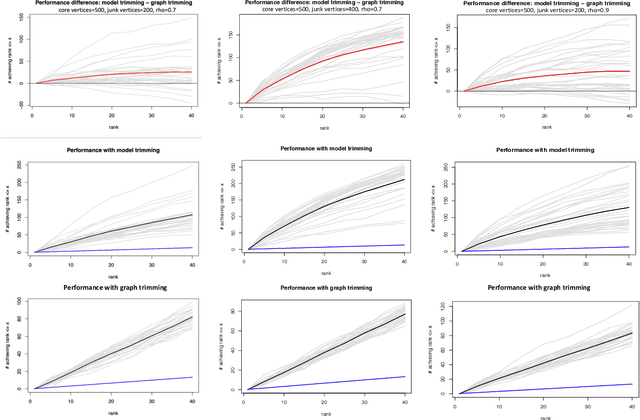
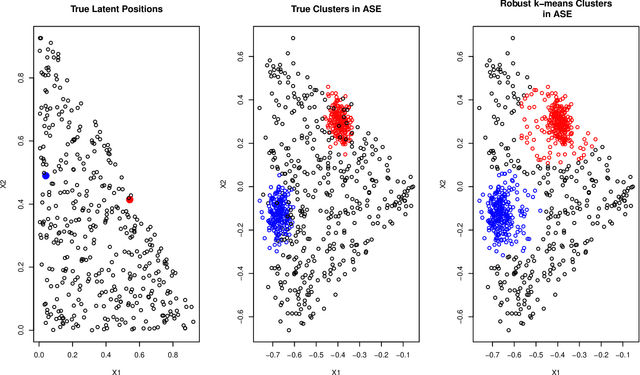
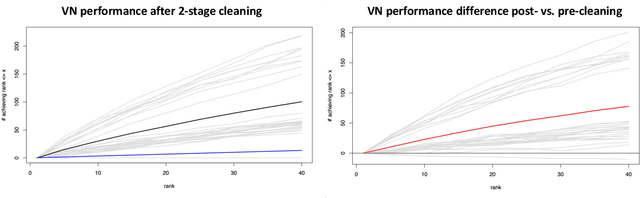
As graph data becomes more ubiquitous, the need for robust inferential graph algorithms to operate in these complex data domains is crucial. In many cases of interest, inference is further complicated by the presence of adversarial data contamination. The effect of the adversary is frequently to change the data distribution in ways that negatively affect statistical and algorithmic performance. We study this phenomenon in the context of vertex nomination, a semi-supervised information retrieval task for network data. Here, a common suite of methods relies on spectral graph embeddings, which have been shown to provide both good algorithmic performance and flexible settings in which regularization techniques can be implemented to help mitigate the effect of an adversary. Many current regularization methods rely on direct network trimming to effectively excise the adversarial contamination, although this direct trimming often gives rise to complicated dependency structures in the resulting graph. We propose a new trimming method that operates in model space which can address both block structure contamination and white noise contamination (contamination whose distribution is unknown). This model trimming is more amenable to theoretical analysis while also demonstrating superior performance in a number of simulations, compared to direct trimming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge