Advancing Regular Language Reasoning in Linear Recurrent Neural Networks

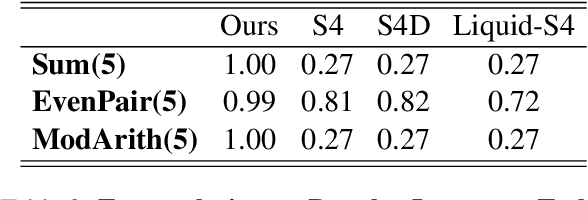
In recent studies, linear recurrent neural networks (LRNNs) have achieved Transformer-level performance in natural language modeling and long-range modeling while offering rapid parallel training and constant inference costs. With the resurged interest in LRNNs, we study whether they can learn the hidden rules in training sequences, such as the grammatical structures of regular language. We theoretically analyze some existing LRNNs and discover their limitations on regular language. Motivated by the analysis, we propose a new LRNN equipped with a block-diagonal and input-dependent transition matrix. Experiments suggest that the proposed model is the only LRNN that can perform length extrapolation on regular language tasks such as Sum, Even Pair, and Modular Arithmetic.