ADS: Approximate Densest Subgraph for Novel Image Discovery
Paper and Code
Feb 13, 2024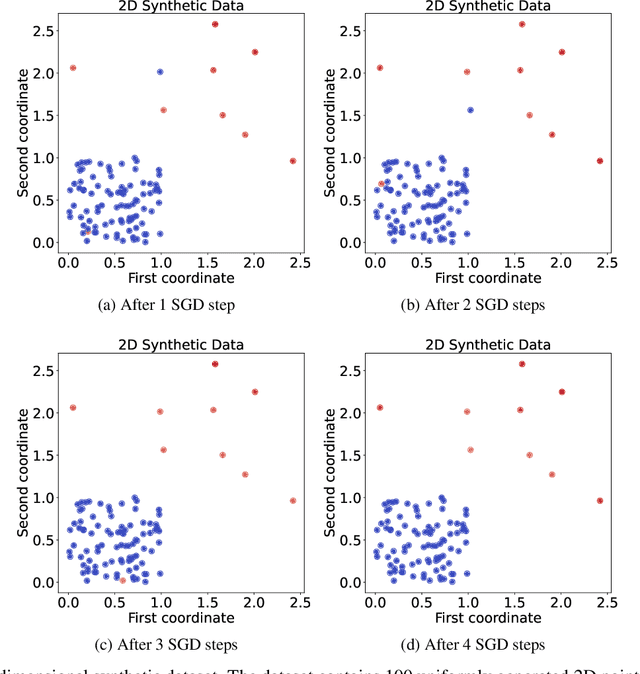
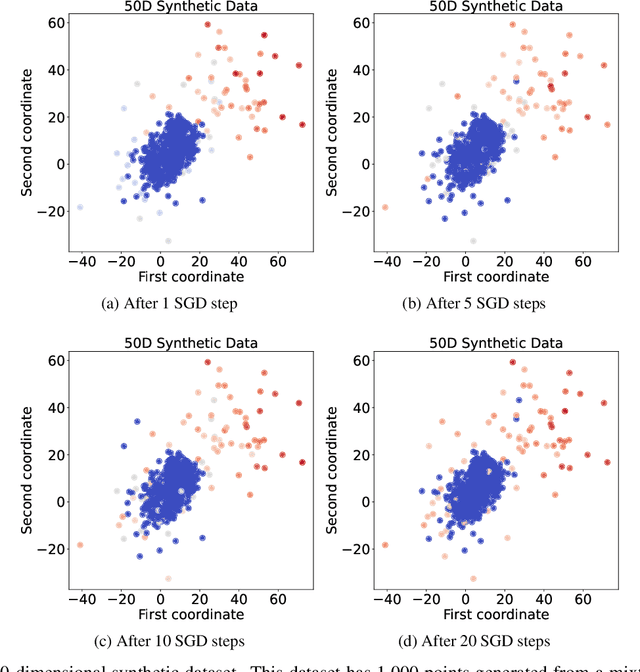
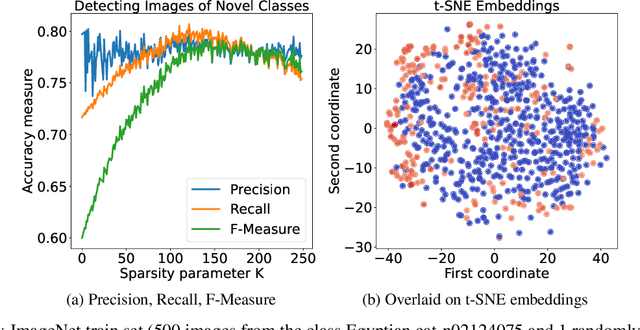
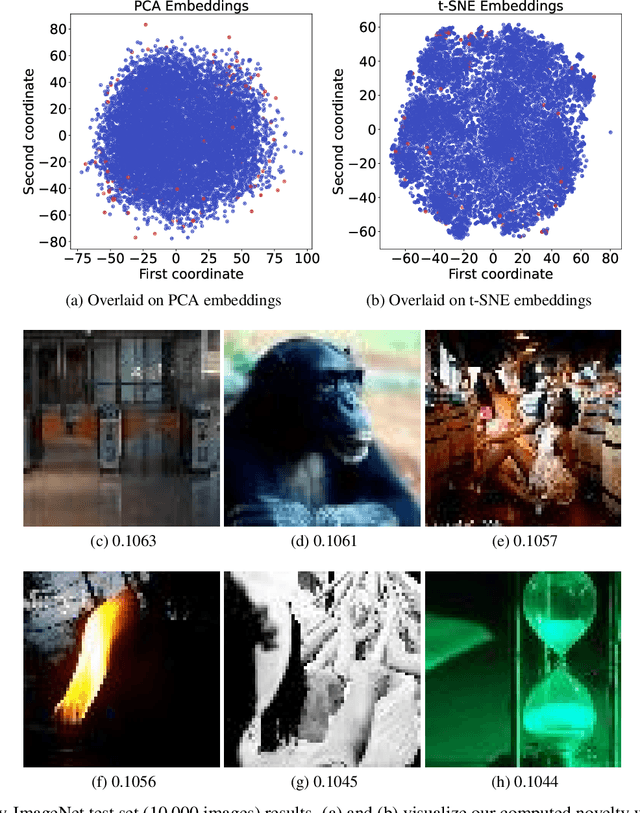
The volume of image repositories continues to grow. Despite the availability of content-based addressing, we still lack a lightweight tool that allows us to discover images of distinct characteristics from a large collection. In this paper, we propose a fast and training-free algorithm for novel image discovery. The key of our algorithm is formulating a collection of images as a perceptual distance-weighted graph, within which our task is to locate the K-densest subgraph that corresponds to a subset of the most unique images. While solving this problem is not just NP-hard but also requires a full computation of the potentially huge distance matrix, we propose to relax it into a K-sparse eigenvector problem that we can efficiently solve using stochastic gradient descent (SGD) without explicitly computing the distance matrix. We compare our algorithm against state-of-the-arts on both synthetic and real datasets, showing that it is considerably faster to run with a smaller memory footprint while able to mine novel images more accurately.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge