Adaptive Submodular Ranking

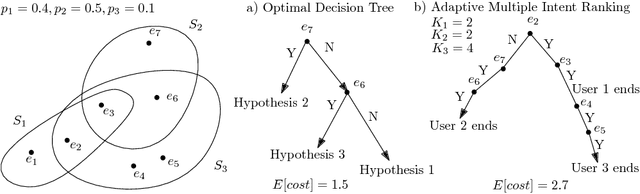
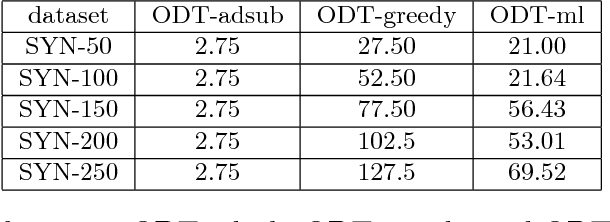
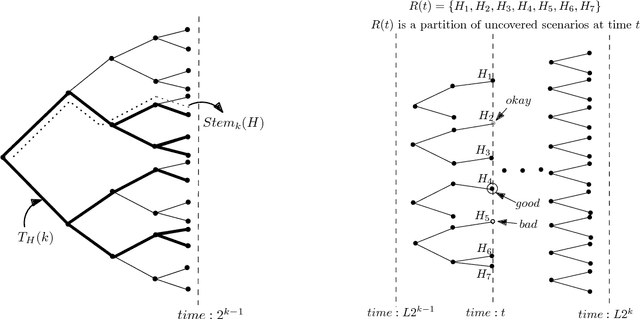
We study a general adaptive ranking problem where an algorithm needs to perform a sequence of actions on a random user, drawn from a known distribution, so as to "satisfy" the user as early as possible. The satisfaction of each user is captured by an individual submodular function, where the user is said to be satisfied when the function value goes above some threshold. We obtain a logarithmic factor approximation algorithm for this adaptive ranking problem, which is the best possible. The adaptive ranking problem has many applications in active learning and ranking: it significantly generalizes previously-studied problems such as optimal decision trees, equivalence class determination, decision region determination and submodular cover. We also present some preliminary experimental results based on our algorithm.