Adaptive Resolution Residual Networks -- Generalizing Across Resolutions Easily and Efficiently

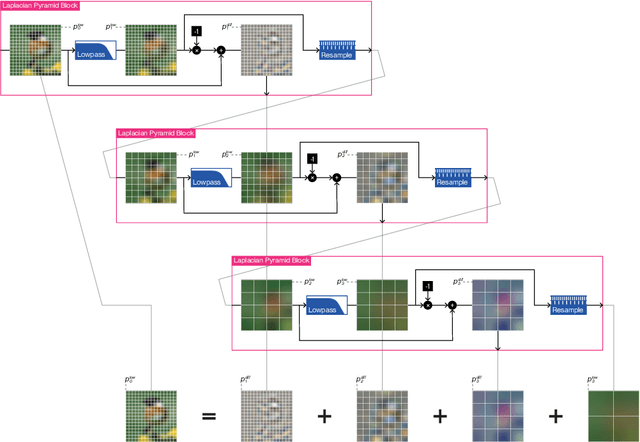
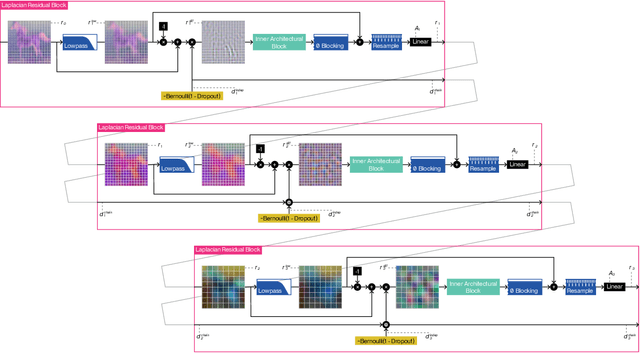
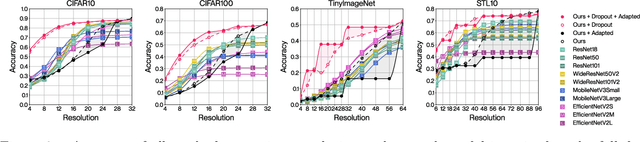
The majority of signal data captured in the real world uses numerous sensors with different resolutions. In practice, however, most deep learning architectures are fixed-resolution; they consider a single resolution at training time and inference time. This is convenient to implement but fails to fully take advantage of the diverse signal data that exists. In contrast, other deep learning architectures are adaptive-resolution; they directly allow various resolutions to be processed at training time and inference time. This benefits robustness and computational efficiency but introduces difficult design constraints that hinder mainstream use. In this work, we address the shortcomings of both fixed-resolution and adaptive-resolution methods by introducing Adaptive Resolution Residual Networks (ARRNs), which inherit the advantages of adaptive-resolution methods and the ease of use of fixed-resolution methods. We construct ARRNs from Laplacian residuals, which serve as generic adaptive-resolution adapters for fixed-resolution layers, and which allow casting high-resolution ARRNs into low-resolution ARRNs at inference time by simply omitting high-resolution Laplacian residuals, thus reducing computational cost on low-resolution signals without compromising performance. We complement this novel component with Laplacian dropout, which regularizes for robustness to a distribution of lower resolutions, and which also regularizes for errors that may be induced by approximate smoothing kernels in Laplacian residuals. We provide a solid grounding for the advantageous properties of ARRNs through a theoretical analysis based on neural operators, and empirically show that ARRNs embrace the challenge posed by diverse resolutions with greater flexibility, robustness, and computational efficiency.