Active Tuples-based Scheme for Bounding Posterior Beliefs
Paper and Code
Jan 16, 2014
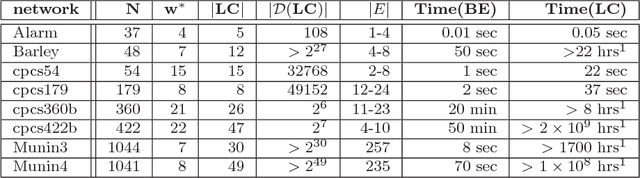

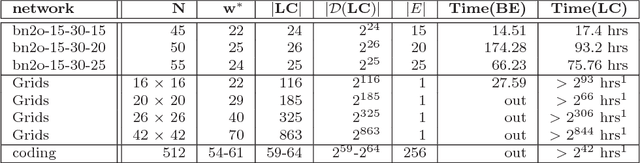
The paper presents a scheme for computing lower and upper bounds on the posterior marginals in Bayesian networks with discrete variables. Its power lies in its ability to use any available scheme that bounds the probability of evidence or posterior marginals and enhance its performance in an anytime manner. The scheme uses the cutset conditioning principle to tighten existing bounding schemes and to facilitate anytime behavior, utilizing a fixed number of cutset tuples. The accuracy of the bounds improves as the number of used cutset tuples increases and so does the computation time. We demonstrate empirically the value of our scheme for bounding posterior marginals and probability of evidence using a variant of the bound propagation algorithm as a plug-in scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge