A Unified Theory of Quantum Neural Network Loss Landscapes

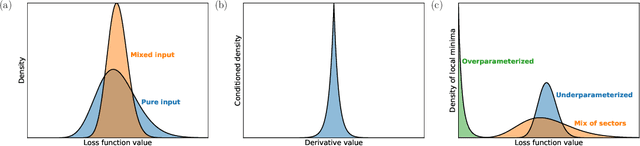
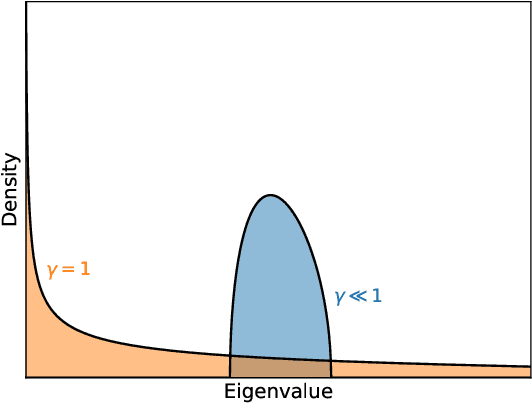
Classical neural networks with random initialization famously behave as Gaussian processes in the limit of many neurons, with the architecture of the network determining the covariance of the associated process. This limit allows one to completely characterize the training behavior of such networks and show that, generally, classical neural networks train efficiently via gradient descent. No such general understanding exists for quantum neural networks (QNNs), which -- outside of certain special cases -- are known to not behave as Gaussian processes when randomly initialized. We here prove that instead QNNs and their first two derivatives generally form what we call Wishart processes, where now certain algebraic properties of the network determine the hyperparameters of the process. This Wishart process description allows us to, for the first time: 1. Give necessary and sufficient conditions for a QNN architecture to have a Gaussian process limit. 2. Calculate the full gradient distribution, unifying previously known barren plateau results. 3. Calculate the local minima distribution of algebraically constrained QNNs. The transition from trainability to untrainability in each of these contexts is governed by a single parameter we call the "degrees of freedom" of the network architecture. We thus end by proposing a formal definition for the "trainability" of a given QNN architecture using this experimentally accessible quantity.