A Unified Framework for Constructing Nonconvex Regularizations
Paper and Code
Jun 11, 2021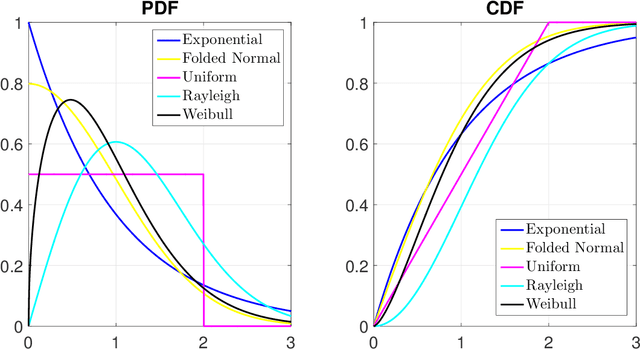
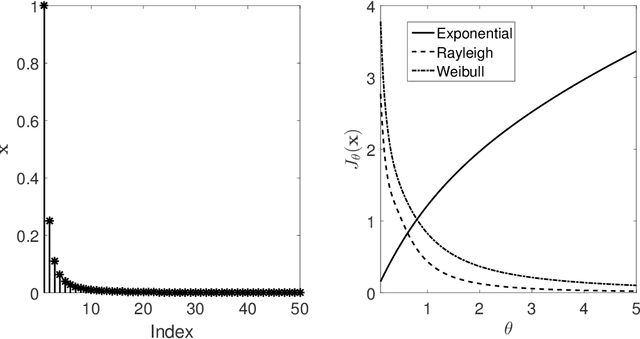
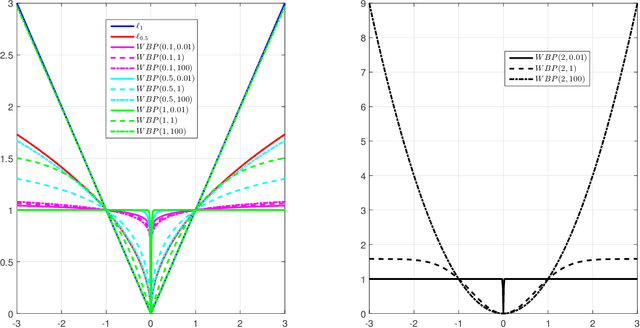
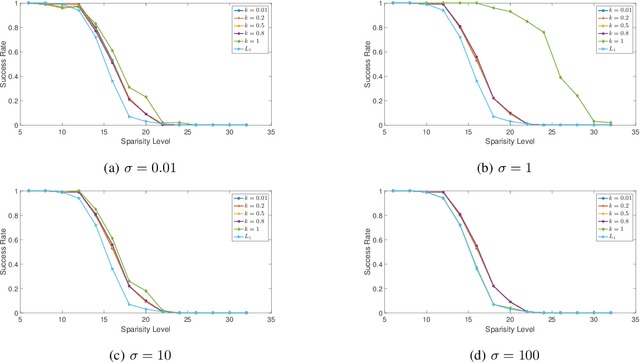
Over the past decades, many individual nonconvex methods have been proposed to achieve better sparse recovery performance in various scenarios. However, how to construct a valid nonconvex regularization function remains open in practice. In this paper, we fill in this gap by presenting a unified framework for constructing the nonconvex regularization based on the probability density function. Meanwhile, a new nonconvex sparse recovery method constructed via the Weibull distribution is studied.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge