A Theoretical Analysis of Fine-tuning with Linear Teachers
Paper and Code
Jul 04, 2021
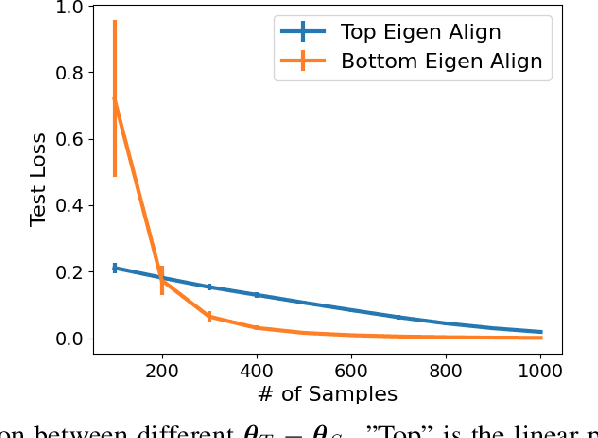
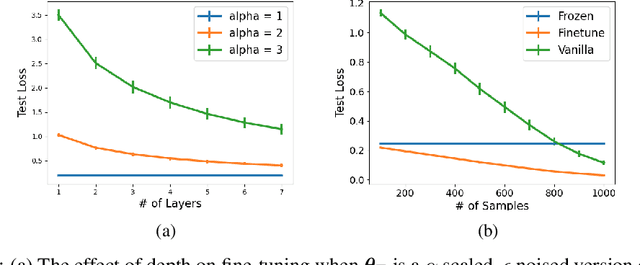
Fine-tuning is a common practice in deep learning, achieving excellent generalization results on downstream tasks using relatively little training data. Although widely used in practice, it is lacking strong theoretical understanding. We analyze the sample complexity of this scheme for regression with linear teachers in several architectures. Intuitively, the success of fine-tuning depends on the similarity between the source tasks and the target task, however measuring it is non trivial. We show that a relevant measure considers the relation between the source task, the target task and the covariance structure of the target data. In the setting of linear regression, we show that under realistic settings a substantial sample complexity reduction is plausible when the above measure is low. For deep linear regression, we present a novel result regarding the inductive bias of gradient-based training when the network is initialized with pretrained weights. Using this result we show that the similarity measure for this setting is also affected by the depth of the network. We further present results on shallow ReLU models, and analyze the dependence of sample complexity there on source and target tasks. We empirically demonstrate our results for both synthetic and realistic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge