A Novel Machine Learning Method for Preference Identification
Paper and Code
Oct 22, 2020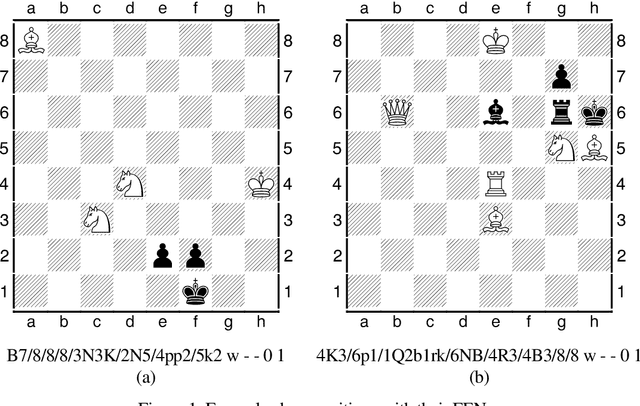
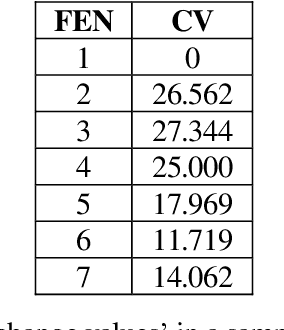
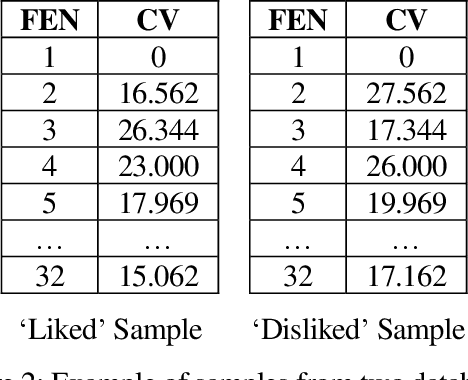
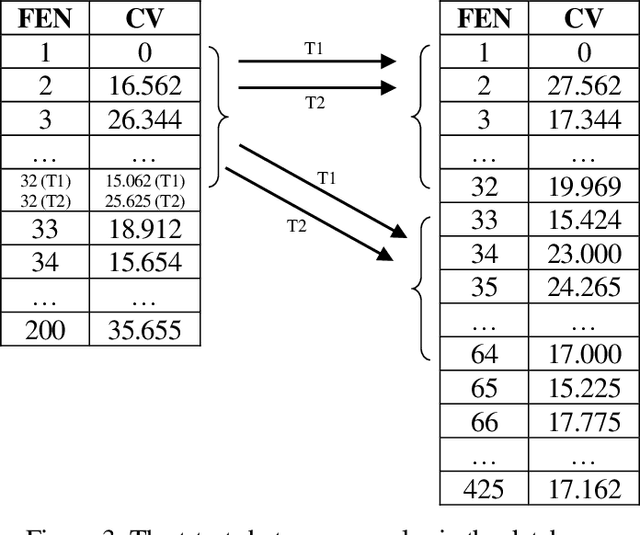
Human preference or taste within any domain is usually a difficult thing to identify or predict with high probability. In the domain of chess problem composition, the same is true. Traditional machine learning approaches tend to focus on the ability of computers to process massive amounts of data and continuously adjust 'weights' within an artificial neural network to better distinguish between say, two groups of objects. Contrasted with chess compositions, there is no clear distinction between what constitutes one and what does not; even less so between a good one and a poor one. We propose a computational method that is able to learn from existing databases of 'liked' and 'disliked' compositions such that a new and unseen collection can be sorted with increased probability of matching a solver's preferences. The method uses a simple 'change factor' relating to the Forsyth-Edwards Notation (FEN) of each composition's starting position, coupled with repeated statistical analysis of sample pairs from both databases. Tested using the author's own collections of computer-generated chess problems, the experimental results showed that the method was able to sort a new and unseen collection of compositions such that, on average, over 70% of the preferred compositions were in the top half of the collection. This saves significant time and energy on the part of solvers as they are likely to find more of what they like sooner. The method may even be applicable to other domains such as image processing because it does not rely on any chess-specific rules but rather just a sufficient and quantifiable 'change' in representation from one object to the next.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge