A Generalized Circuit for the Hamiltonian Dynamics Through the Truncated Series
Paper and Code
Aug 08, 2018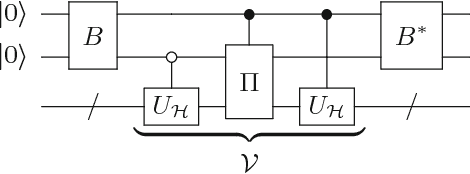

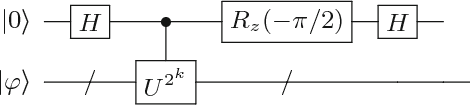
In this paper, we present a method for the Hamiltonian simulation in the context of eigenvalue estimation problems which improves earlier results dealing with Hamiltonian simulation through the truncated Taylor series. In particular, we present a fixed-quantum circuit design for the simulation of the Hamiltonian dynamics, $H(t)$, through the truncated Taylor series method described by Berry et al. \cite{berry2015simulating}. The circuit is general and can be used to simulate any given matrix in the phase estimation algorithm by only changing the angle values of the quantum gates implementing the time variable $t$ in the series. The circuit complexity depends on the number of summation terms composing the Hamiltonian and requires $O(Ln)$ number of quantum gates for the simulation of a molecular Hamiltonian. Here, $n$ is the number of states of a spin orbital, and $L$ is the number of terms in the molecular Hamiltonian and generally bounded by $O(n^4)$. We also discuss how to use the circuit in adaptive processes and eigenvalue related problems along with a slight modified version of the iterative phase estimation algorithm. In addition, a simple divide and conquer method is presented for mapping a matrix which are not given as sums of unitary matrices into the circuit. The complexity of the circuit is directly related to the structure of the matrix and can be bounded by $O(poly(n))$ for a matrix with $poly(n)-$sparsity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge