A generalization of the achievable rate of a MISO system using Bode-Fano wideband matching theory
Paper and Code
Oct 15, 2023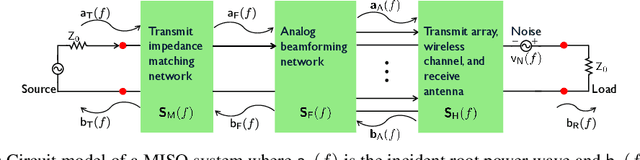

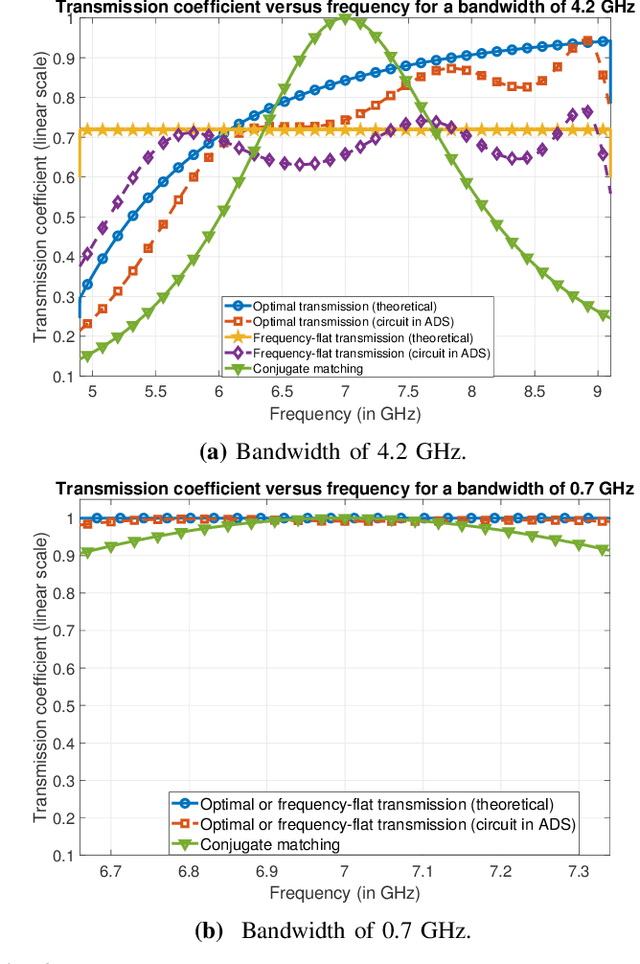
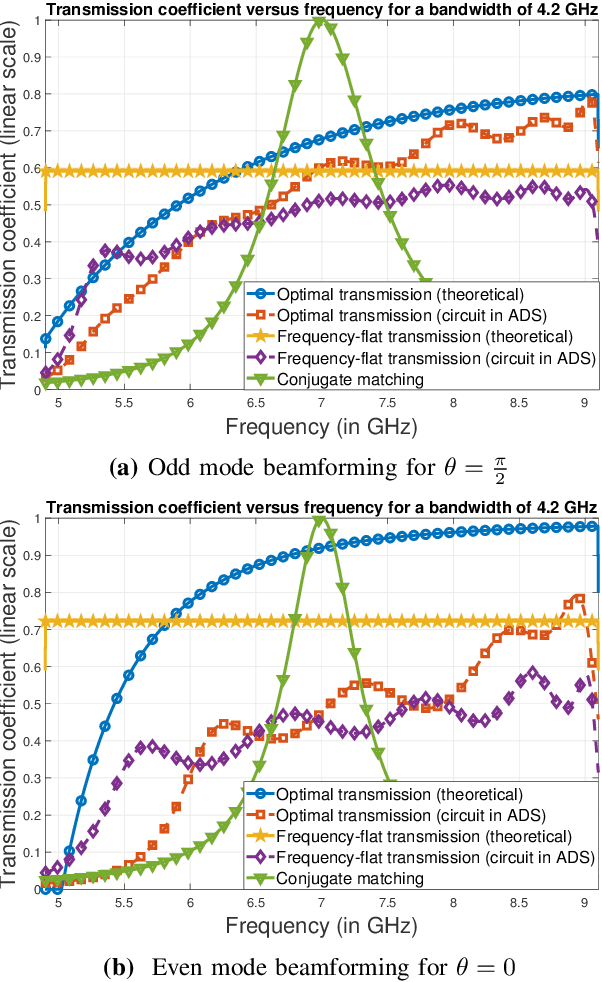
Impedance-matching networks affect power transfer from the radio frequency (RF) chains to the antennas. Their design impacts the signal to noise ratio (SNR) and the achievable rate. In this paper, we maximize the information-theoretic achievable rate of a multiple-input-single-output (MISO) system with wideband matching constraints. Using a multiport circuit theory approach with frequency-selective scattering parameters, we propose a general framework for optimizing the MISO achievable rate that incorporates Bode-Fano wideband matching theory. We express the solution to the achievable rate optimization problem in terms of the optimized transmission coefficient and the Lagrangian parameters corresponding to the Bode-Fano inequality constraints. We apply this framework to a single electric Chu's antenna and an array of two electric Chu's antennas. We compare the optimized achievable rate obtained numerically with other benchmarks like the ideal achievable rate computed by disregarding matching constraints and the achievable rate obtained by using sub-optimal matching strategies like conjugate matching and frequency-flat transmission. We also propose a practical methodology to approximate the achievable rate bound by using the optimal transmission coefficient to derive a physically realizable matching network through the ADS software.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge