A game-theoretic framework for classifier ensembles using weighted majority voting with local accuracy estimates
Paper and Code
Feb 03, 2013
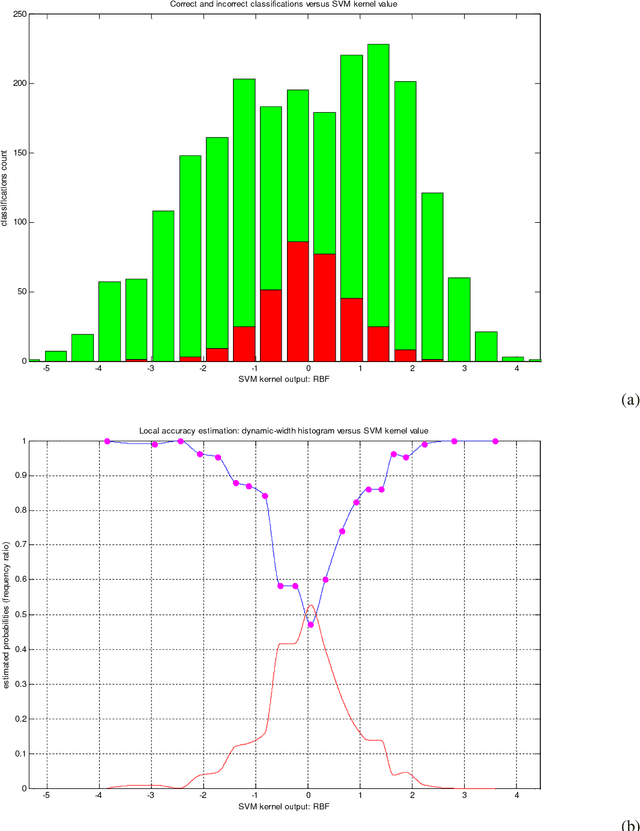
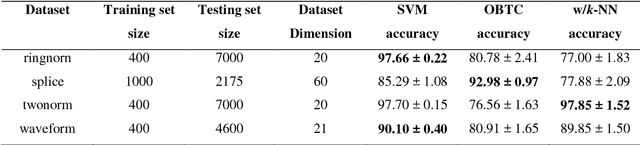

In this paper, a novel approach for the optimal combination of binary classifiers is proposed. The classifier combination problem is approached from a Game Theory perspective. The proposed framework of adapted weighted majority rules (WMR) is tested against common rank-based, Bayesian and simple majority models, as well as two soft-output averaging rules. Experiments with ensembles of Support Vector Machines (SVM), Ordinary Binary Tree Classifiers (OBTC) and weighted k-nearest-neighbor (w/k-NN) models on benchmark datasets indicate that this new adaptive WMR model, employing local accuracy estimators and the analytically computed optimal weights outperform all the other simple combination rules.
* 21 pages, 9 tables, 1 figure, 68 references
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge